Test: Kinetic Theory (29 Sep) - JEE MCQ
15 Questions MCQ Test - Test: Kinetic Theory (29 Sep)
The P-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
The ratio of the adiabatic to isothermal elasticities of a triatomic (non-linear) gas is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The specific heats, Cp and CV of gas of diatomic molecules, A, is given (in units of J mol −1K−1) by 29 and 22, respectively. Another gas of diatomic molecules, B, has the corresponding values 30 and 21. If they are treated as ideal gases, then
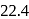 lit at N.T.P. Calculate the difference between two molar specific heats of the gas.
lit at N.T.P. Calculate the difference between two molar specific heats of the gas. 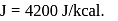
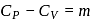 and for the nitrogen
and for the nitrogen 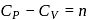 , where
, where 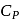 and
and 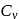 refer to specific heat per unit mass at constant pressure and specific heat per unit mass at constant volume respectively. The relation between
refer to specific heat per unit mass at constant pressure and specific heat per unit mass at constant volume respectively. The relation between 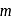 and
and 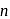 is
is
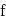 , then the ratio of two specific heats is given by
, then the ratio of two specific heats is given by
The average translational kinetic energy of a molecule in a gas becomes equal to 0.69eV at temperature about, [Boltzmann's constant = 138 × 10−23 J K−1]
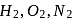 and He are enclosed in identical containers under the similar conditions of pressure and temperature. The gases will have
and He are enclosed in identical containers under the similar conditions of pressure and temperature. The gases will have
Let 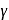 denote the ratio of specific heat for an ideal gas. Then choose the correct expression for number of degrees of freedom of a molecule of the same gas.
denote the ratio of specific heat for an ideal gas. Then choose the correct expression for number of degrees of freedom of a molecule of the same gas.
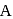 and
and 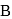 contain an equal quantity of water at
contain an equal quantity of water at 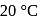 . A
. A 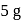 piece of metal
piece of metal 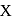 of specific heat
of specific heat 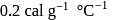 is dropped into
is dropped into 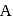 and
and 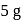 piece of metal
piece of metal 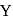 is dropped into
is dropped into 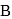 . The equilibrium temperature in
. The equilibrium temperature in 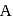 is
is 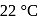 and that in
and that in 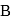 is
is 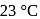 . The initial temperature of both the metals was
. The initial temperature of both the metals was 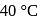 . The specific heat of metal
. The specific heat of metal 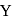 (in
(in 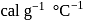 ) is
) is
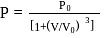 , where
, where 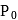 and
and 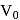 are constants. The translational kinetic energy of the gas when
are constants. The translational kinetic energy of the gas when 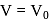 is given by
is given by
Temperature at which the kinetic energy of gas molecule is half of the value of kinetic energy at 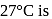
A nitrogen molecule has some rms speed at 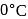 on the surface of the earth. With this speed, it goes straight up. If there is no collisions with other molecules, the molecule will rise up to a height of
on the surface of the earth. With this speed, it goes straight up. If there is no collisions with other molecules, the molecule will rise up to a height of
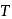 is the root mean square speed of a hydrogen molecule equal to its escape velocity from the surface of the moon? The radius of moon is
is the root mean square speed of a hydrogen molecule equal to its escape velocity from the surface of the moon? The radius of moon is 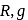 is the acceleration due to gravity on moon's surface,
is the acceleration due to gravity on moon's surface, 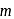 is the mass of a hydrogen molecule and
is the mass of a hydrogen molecule and 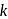 is the Boltzmann constant
is the Boltzmann constant


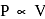 or
or 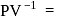 constant Molar heat capacity in the process
constant Molar heat capacity in the process 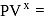 constant is
constant is 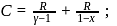 Here
Here 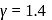 (For diatomic gas)
(For diatomic gas) 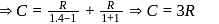
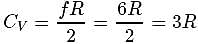
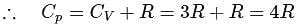
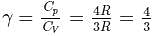
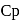 and
and  of A are 29 and 22 and
of A are 29 and 22 and 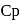 and
and 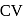 of
of 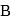 are 30 and
are 30 and 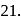
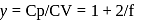
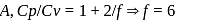
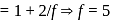
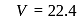 litre
litre 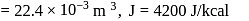
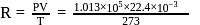
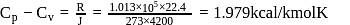
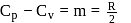
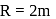
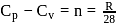 or
or 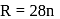
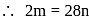
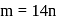
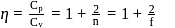
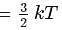
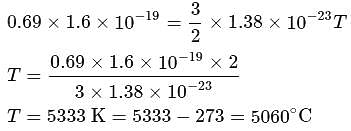
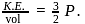 Here
Here  is constant
is constant = Total Energy,
= Total Energy,  = Degree of freedom of molecule, We Know,
= Degree of freedom of molecule, We Know,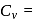 Molar heat capacity at constant volume
Molar heat capacity at constant volume 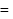
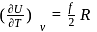
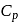 = Molar heat capacity at constant pressure
= Molar heat capacity at constant pressure 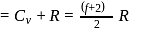
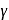 = Ratio of specific heats
= Ratio of specific heats 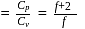
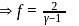
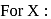
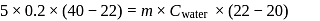
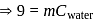
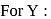
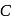 be the specific heat of the metal
be the specific heat of the metal 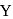 , then
, then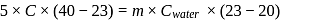
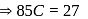
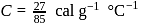
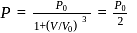
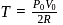
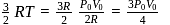
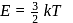
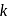 is Boltzmann's constant.
is Boltzmann's constant.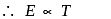
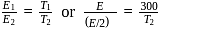
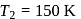
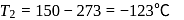
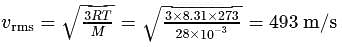
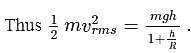
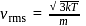
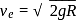
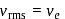 , we require
, we require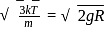 or
or 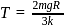 , which is choice (d).
, which is choice (d).














