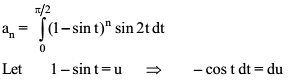Test: Definite Integration: Leibnitz Theorem (3 Oct) - JEE MCQ
10 Questions MCQ Test - Test: Definite Integration: Leibnitz Theorem (3 Oct)
Let f(x) = sin(x)/1+x2. Let y(n) denote the nth derivative of f(x) at x = 0 then the value of y(100) + 9900y(98) is
Let f(x) = ln(x)/x+1 and let y(n) denote the nth derivative of f(x) at x = 1 then the value of 2y(100) + 100y(99)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let f(x) = 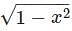 and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) is
and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) is
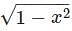 and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) is
and let y(n) denote the nth derivative of f(x) at x = 0 then the value of 6y (1) y(2) + 2y(3) isLet f(x) = tan(x) and let y(n) denote the nth derivative of f(x) then the value of y(9998879879789776) is
If the first and second derivatives at x = 0 of the function f(x)=  were 2 and 3 then the value of the third derivative is
were 2 and 3 then the value of the third derivative is
For the given function f(x)= 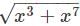 the values of first and second derivative at x = 1 are assumed as 0 and 1 respectively. Then the value of the third derivative could be
the values of first and second derivative at x = 1 are assumed as 0 and 1 respectively. Then the value of the third derivative could be
Let f(x)=  and let the nth derivative at x = 0 be given by y(n) Then the value of the expression for y(n) is given by
and let the nth derivative at x = 0 be given by y(n) Then the value of the expression for y(n) is given by
Let f(x) = ex sinh(x) / x, let y(n) denote the nth derivative of f(x) at x = 0 then the expression for y(n) is given by


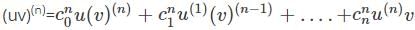

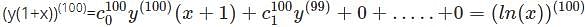
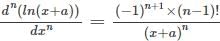
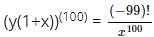
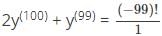
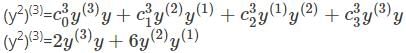
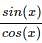
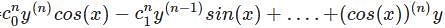
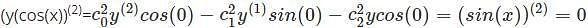
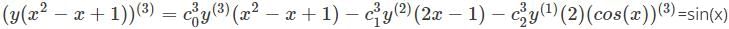


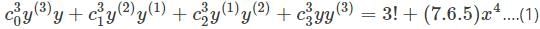
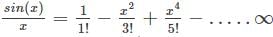
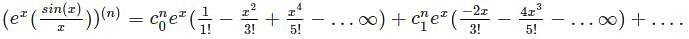

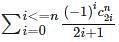 is the right answer.
is the right answer.
 applying the Leibniz rule for nth derivative we have
applying the Leibniz rule for nth derivative we have