Test: Biot-Savart Law(1 Dec) - JEE MCQ

As,
B=μ_onI/2a
a ->radius
B ∝1/a
B₁/B₂=a₂/a₁
B₁=2B₂
B₂=(1/2) x B₁,
Magnetic field is halved.

Correct answer is A.

dB=μ_oidlsin90/4πr²=μ_oidl/4πr²
B_net= ∫dBsinθ
      = ∫μ_oidlR/4πr²r== (μ_oiR/4πr³) ∫dl
      = (μ_oiR/4πr³)2πR= μ_oiR²/2(R²+x²)^3/2
   B= μ_oiR²/2(R2+x²)^3/2
If x>>>R
B= μ_oiR²/2(x²)^3/2

[=B ∝ x^-3]

The magnetic field produced by a current-carrying coil at its center is given by the formula,
B = μ0 * (N*I/R),
where,
B is the magnetic field,
μ0 is the permeability of free space,
N is the number of turns in the coil,
I is the current through the coil, and
R is the radius of the coil.
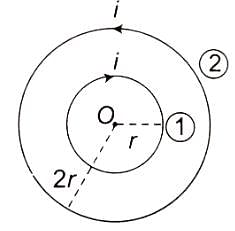
In this case, both the coils carry the same current but in opposite directions. So, the fields produced by them will be in opposite directions. Also, the diameter of the inner coil is half that of the outer coil. Thus, the radius of the inner coil will be half that of the outer coil.
Therefore, the field at the center due to the inner coil will be double that due to the outer coil (because the magnetic field is inversely proportional to the radius).
Since the fields are in opposite directions, the net field at the center will be the difference between the two fields. That is, 2B (due to the inner coil) - B (due to the outer coil) = B.
So, if the field due to the outer coil is 1 T (Tesla), the net field at the center will also be 1 T.
Hence, the correct answer is 3. 1T.

From Biot-Savart law, magnetic field at a point p, B= (μ0​/4π)∫ [(Idl×r​)/ r3]
where r is the distance of point p from conductor and I is the current in the conductor.
Thus magnetic field due to current carrying conductor depends on the current flowing through conductor and distance from the conductor and length of the conductor.
 

B= 2μ₀​i⋅πr²/4π(r²+x²)^3/2
Magnetic field at centre= μ₀​i/2r
B= μ₀​i/2r
Put r= √3
B¹=2μ_0​i⋅πr²/4π(4r²)^3/2
=B/8
Hence, √3R distance from the centre magnetic field is equal to magnetic field at centre 
 

The magnetic field due to a circular loop is given by:
B= μ₀​​2πi​/4πr
=10⁻⁷×2π×2/0.0157 ​
=8×10⁻⁵ Wb/m²

The magnetic field at the center O due to the upper side of the semicircular current loop is equal and opposite to that due to the lower side of the loop.

 B=μ₀2πnIa²/4π (a²+x²)^3/2
=10⁻⁷×2×(22/7)×200×5×(0⋅1/2)²/ [(0⋅1/2)²+(0⋅15)²]^3/2
=39.74x10^-5
 

Let the radii be r₁​ and r₂​ respectively.
Since there are two turns of radius r₂​, r₁​=2r_2​
Magnetic field B at the centre of  the coil of radius r_1​ B_1​=​μo​i/2r₁​=​μ_o​i​/4r₂
Magnetic field B at the center of the coil of radius r_2​ B_2​=2×​μ_o​i​/2r₂
∴ B₂/B₁ =(2× μ_o​i/2r₂​)/(μ_o​i /4r₂​)​ ​​=4
Hence the answer is option C, four times its initial value.