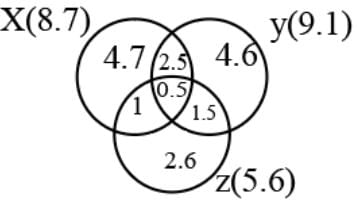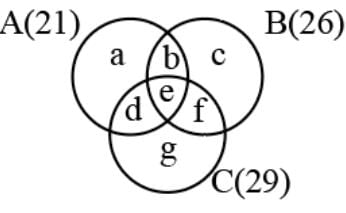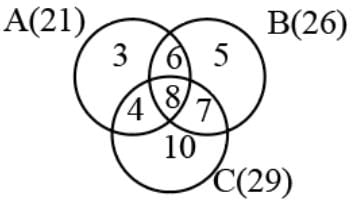Explore Exams
Login Signup
Sign in Open App
CAT Exam  >  CAT Tests  >  Test: Venn Diagrams- 3 - CAT MCQ

Test: Venn Diagrams- 3 - CAT MCQ


Test Description

10 Questions MCQ Test - Test: Venn Diagrams- 3

Test: Venn Diagrams- 3 for CAT 2025 is part of CAT preparation. The Test: Venn Diagrams- 3 questions and answers have been prepared according to the CAT exam syllabus.The Test: Venn Diagrams- 3 MCQs are made for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Venn Diagrams- 3 below.
Solutions of Test: Venn Diagrams- 3 questions in English are available as part of our course for CAT & Test: Venn Diagrams- 3 solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test: Venn Diagrams- 3 | 10 questions in 20 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
Test: Venn Diagrams- 3 - Question 1
Save

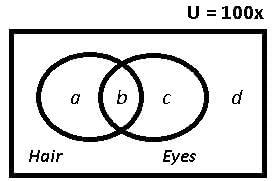
In a certain town, 40% of people have brown hair, 30% of people have brown eyes and 12% have both brown hair and brown eyes. How many people in town have neither brown hair nor brown eyes?

Detailed Solution for Test: Venn Diagrams- 3 - Question 1


Let total number of people in the town = 100x
People who have both brown hair and eyes = b = 12x
⇒ People who have brown hair = a+ b = 40x
⇒ a = 28x
Similarly, c = 18x
∴ People who have neither brown hair nor brown eyes = 100x -(12x + 18x + 28x) = 42%

Test: Venn Diagrams- 3 - Question 2
Save

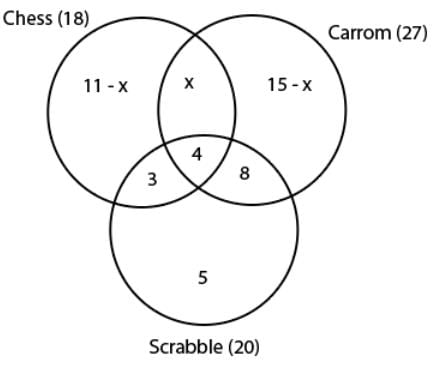
Each student in a class of 40 plays at least one indoor game-chess, carom and scrabble. 18 play chess, 20 play scrabble and 27 play carom. 7 play both chess and scrabble, 12 play both scrabble and carom and 4 play all 3 games. The number of players who play chess and carom but not scrabble is

Detailed Solution for Test: Venn Diagrams- 3 - Question 2

Students who play all the three games are 4, and with the rest information given in the question, we can at best draw the venn diagram as:

Now, total students = 40.

So, Chess+ 5 + 8 + 15 - x = 40

=> 18 + 28 - x = 40

=> 46 - x = 40

∴ x = 6

Clear all your doubts with EduRev
Test: Venn Diagrams- 3 - Question 3
Save

Read the information given below and answer the 2 associated questions.

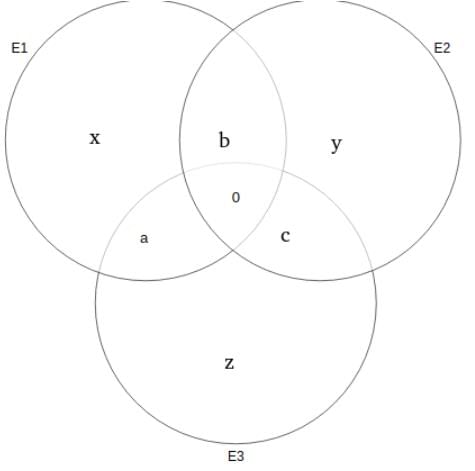
190 students have to choose at least one elective and at most two electives from a list of three electives: E1, E2 and E3. It is found that the number of students choosing E1 is half the number of students choosing E2, and one third the number of students choosing E3.
Moreover, the number of students choosing two electives is 50.

In addition to the given information, which of the following information is NECESSARY and SUFFICIENT to compute the number of students choosing only E1, only E2 and only E3?

Detailed Solution for Test: Venn Diagrams- 3 - Question 3

Given, a + b + c = 50 and a + b + c + x + y + z = 190 => x + y + z = 140.

Also, let E1 = k => E2 = 2k and E3 = 3k

E1 + E2 + E3 = 6k = 190 + 50 = 240 => k = 40.

Option A: If the number of students choosing only E2, the number of students
choosing both E2 and E3, are given then the number of students who choose E2 and E1, E1 and E3 can be found. From this only E1, only E3 can be calculated.

Option B: knowing the number of students choosing both E1 and E2, the number of students
choosing both E2 and E3, and a number of students choosing both E3 and E1 is insufficient. This information is not enough to calculate the number of students who choose only E1, only E2, and only E3.

Option C: If x and c are known, we can’t find y and z.

Option D is not sufficient.

Test: Venn Diagrams- 3 - Question 4
Save

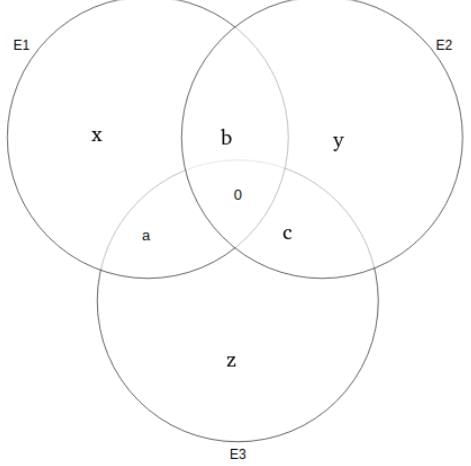
Read the information given below and answer the 2 associated questions.

190 students have to choose at least one elective and at most two electives from a list of three electives: E1, E2 and E3. It is found that the number of students choosing E1 is half the number of students choosing E2, and one third the number of students choosing E3.
Moreover, the number of students choosing two electives is 50.

Which of the following CANNOT be obtained from the given information?
Detailed Solution for Test: Venn Diagrams- 3 - Question 4


Given, a + b + c = 50 and a + b + c + x + y + z = 190 => x + y + z = 140.

Also, let E1 = k => E2 = 2k and E3 = 3k

E1 + E2 + E3 = 6k = 190 + 50 = 240 => k = 40.

Option A,  the number of students choosing E1 is 40.

Option B, number of students choosing either E1 or E2 or both, but not E3 = total – E3 = 190-120 = 70.

Option C, number of students choosing both E1 and E2 => this can not be obtained.

Option D, number of students choosing E3 = 3x = 120.

Test: Venn Diagrams- 3 - Question 5
Save

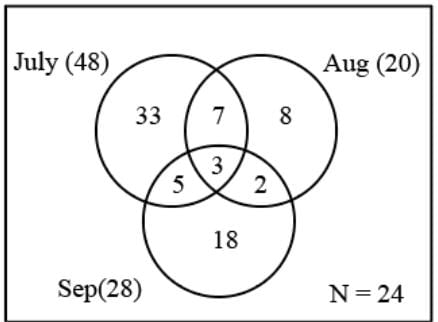
The number of people (in lakhs) who read only one newspaper is
Detailed Solution for Test: Venn Diagrams- 3 - Question 5

Given Readership of newspaper X = 8.7

only X + 2.5 + 0.5 + 1 = 8.7

only X = 4.7

Given Readership of newspaper Y = 9.1

only Y + 2.5 + 1.5 + 0.5 = 9.1

only Y = 4.6

Given Readership of newspaper Z = 5.6

only Z + 0.5 + 1 + 1.5 = 5.6

only Z = 2.6


Number of people who read only one newspaper = 4.7 + 4.6 + 2.6 = 11.9 lakhs

Test: Venn Diagrams- 3 - Question 6
Save

A survey was conducted of 100 people whether they have read recent issues of ‘Golmal’, a monthly magazine. Summarized information is presented below :
Only September: 18
September but not August: 23
September and July: 8
September: 28
July: 48
July and August: 10
None of the three months: 24
What is the number of surveyed people who have read exactly for two consecutive months?
Detailed Solution for Test: Venn Diagrams- 3 - Question 6

Exactly two consecutive months include both July-August and August-September. We cannot include July-September, as these months are not consecutive.

N – none of the three months

Number of people who read in July and August only = 7

Number of people who read in August and September only = 2

Therefore, the number of surveyed people who have read exactly for two consecutive months = 7+2 = 9

Test: Venn Diagrams- 3 - Question 7
Save

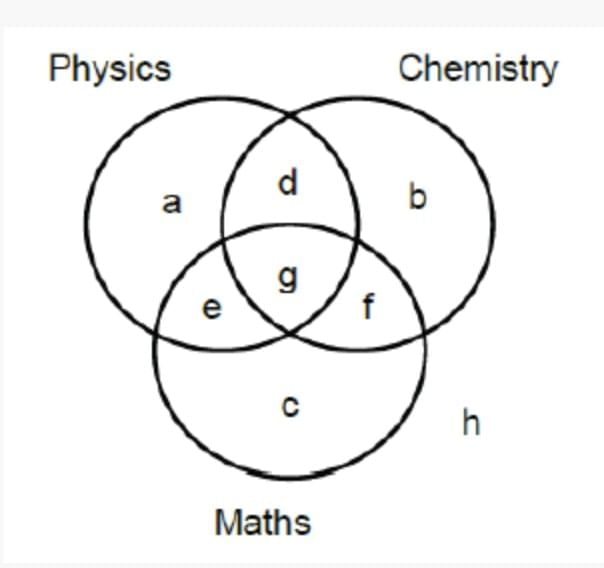
Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection. For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1. No one is below the 80th percentile in all 3 sections.
2. 150 are at or above the 80th percentile in exactly two sections.
3. The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4. Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.


Question: What best can be concluded about the number of candidates sitting for the separate test for BIE who were at or above the 90th percentile overall in CET? 
Detailed Solution for Test: Venn Diagrams- 3 - Question 7

 

It is given that 200 candidates scored above 90th percentile overall in CET. Let the following Venn diagram represent the number of persons who scored above 80 percentile in CET in each of the three sections:

From 1, h = 0.
From 2, d + e + f = 150
From 3, a = b = c
Since there are a total of 200 candidates, 3a + g = 200 – 150 = 50
From 4, (2a + f) : (2a + e) : (2a + d) = 4 : 2 : 1
Therefore, 6a + (d + e + f) is divisible by 4 + 2 + 1 = 7.
Since d + e + f = 150, 6a + 150 is divisible by 7, i.e., 6a + 3 is divisible by 7. Hence, a = 3, 10, 17, . . .
Further, since 3a + g = 5 0, a must be less than 17. Therefore, only two cases are possible for the value of a, i.e., 3 or 10.
We can calculate the values of the other variables for the two cases.
a = 3 or 10
d = 18 or 10
e = 42 or 40
f = 90 or 100
g = 41 or 20

The number of candidates sitting for separate test for BIE who were at or above 90th percentile in CET (a) is either 3 or 10.

Test: Venn Diagrams- 3 - Question 8
Save

During the placement season of a class, 21 students got shortlisted for company A, 26 got shortlisted for Company B and 29 got shortlisted for company C and 14 students got shortlisted for both A and B, 12 students got shortlisted for A and C and 15 for both B and C. All the companies shortlisted 8 students from the class. Then what is the ratio of number of students who got shortlisted for only B and number of students who got shortlisted for only C?
Detailed Solution for Test: Venn Diagrams- 3 - Question 8


Given e = 8

Number of students shortlisted for A and B is 14

e + b = 14

b = 6

Number of students shortlisted for A and C is 12

e + d = 12

d = 4

Number of students shortlisted for B and C is 15

e + f = 15

f = 7

Given

Number of students shortlisted for B is 26

b + f + e + c = 26

6 + 7 + 8 + c = 26

c = 5

Number of students shortlisted for C is 29

d + e + f + g = 29

g = 10

Number of students shortlisted for A is 21

b + e + d + a = 21

a = 3


Number of students shortlisted for only B = c = 5

Number of students shortlisted for only C = g = 10

Ratio = 5:10 = 1:2

Test: Venn Diagrams- 3 - Question 9
Save

In a college, 200 students are randomly selected. 140 like tea, 120 like coffee, and 80 like both tea and coffee.

  • How many students like at least one of the beverages?
Detailed Solution for Test: Venn Diagrams- 3 - Question 9

The following Venn diagram may represent the given information, where T = tea and C = coffee.

  • Number of students who like only tea = 60
  • Number of students who like only coffee = 40
  • Number of students who like at least one of tea or coffee = n (only Tea) + n (only coffee) + n (both Tea & coffee) . So, 60 + 40 + 80 = 180
Test: Venn Diagrams- 3 - Question 10
Save

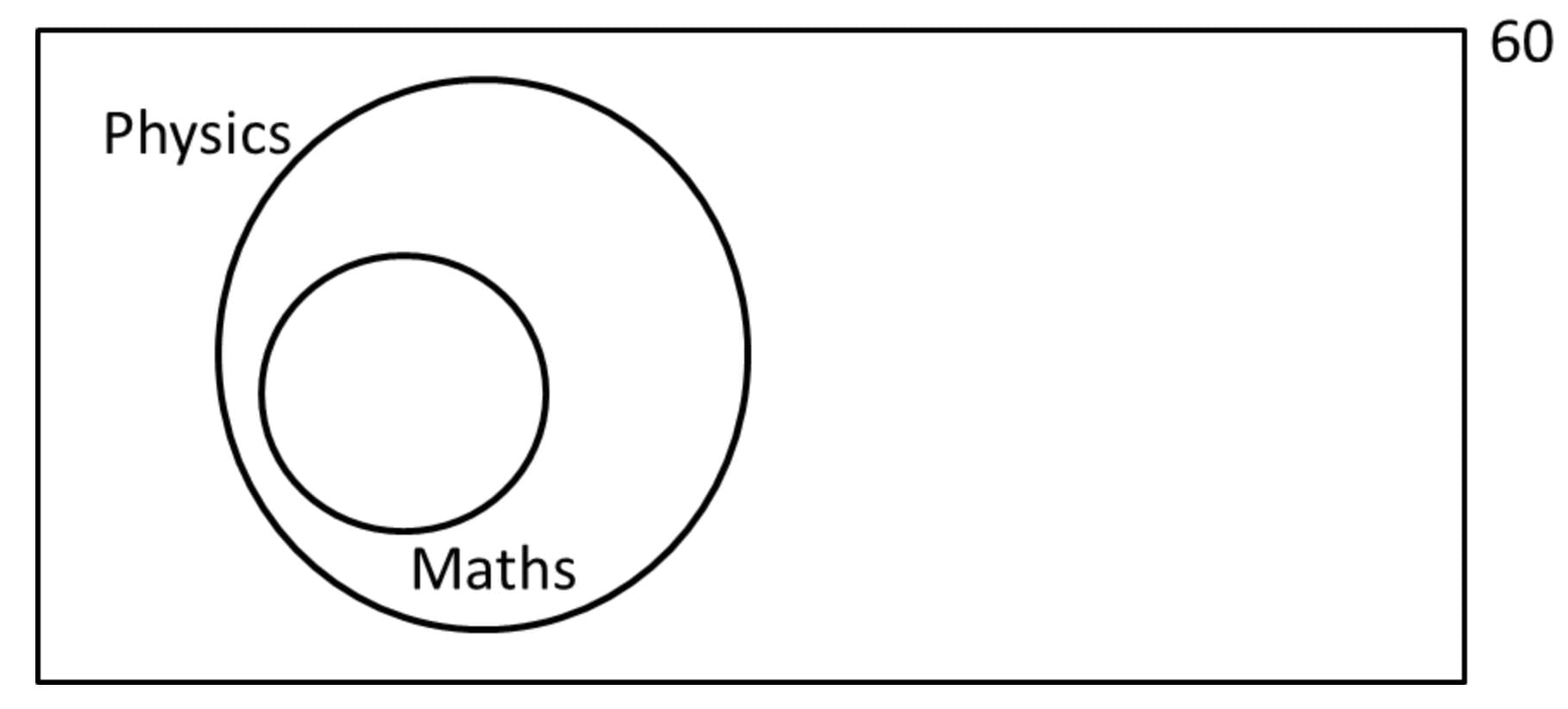
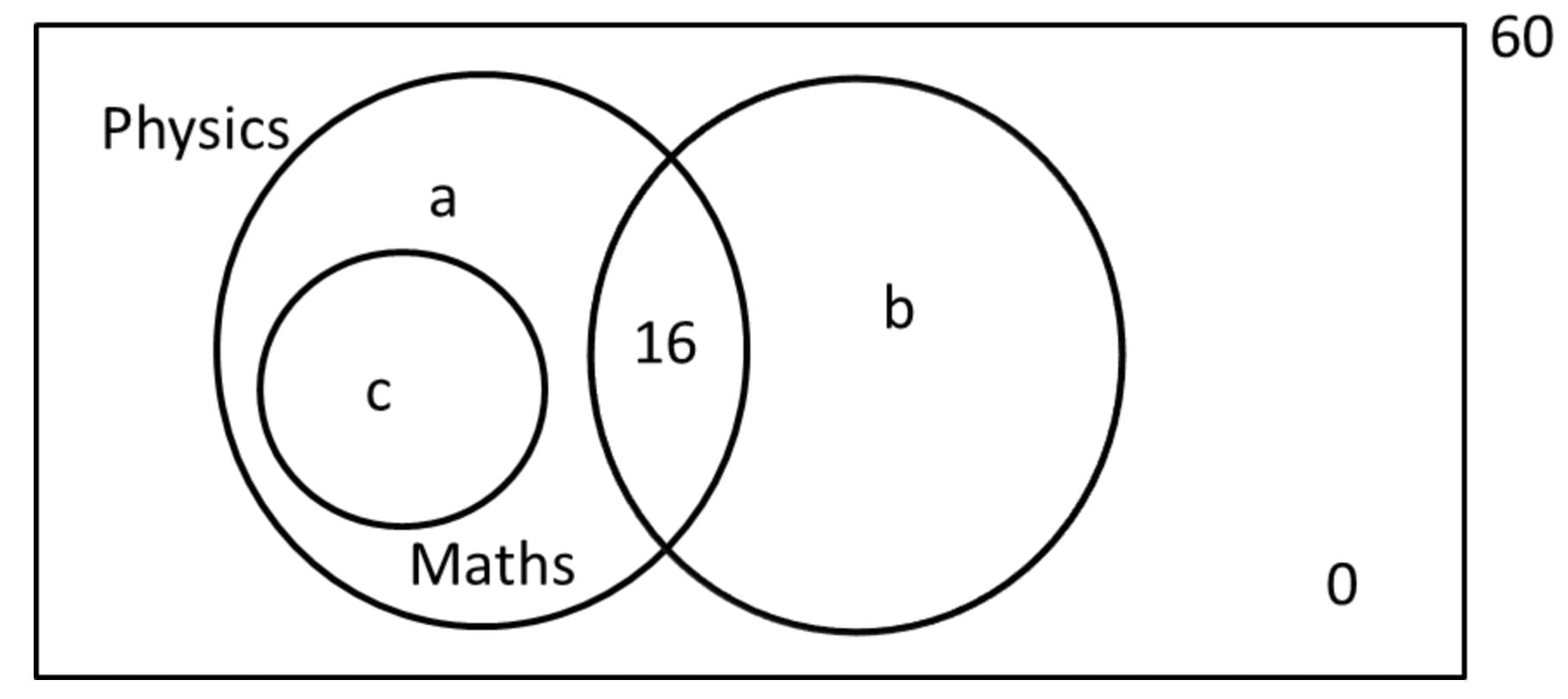
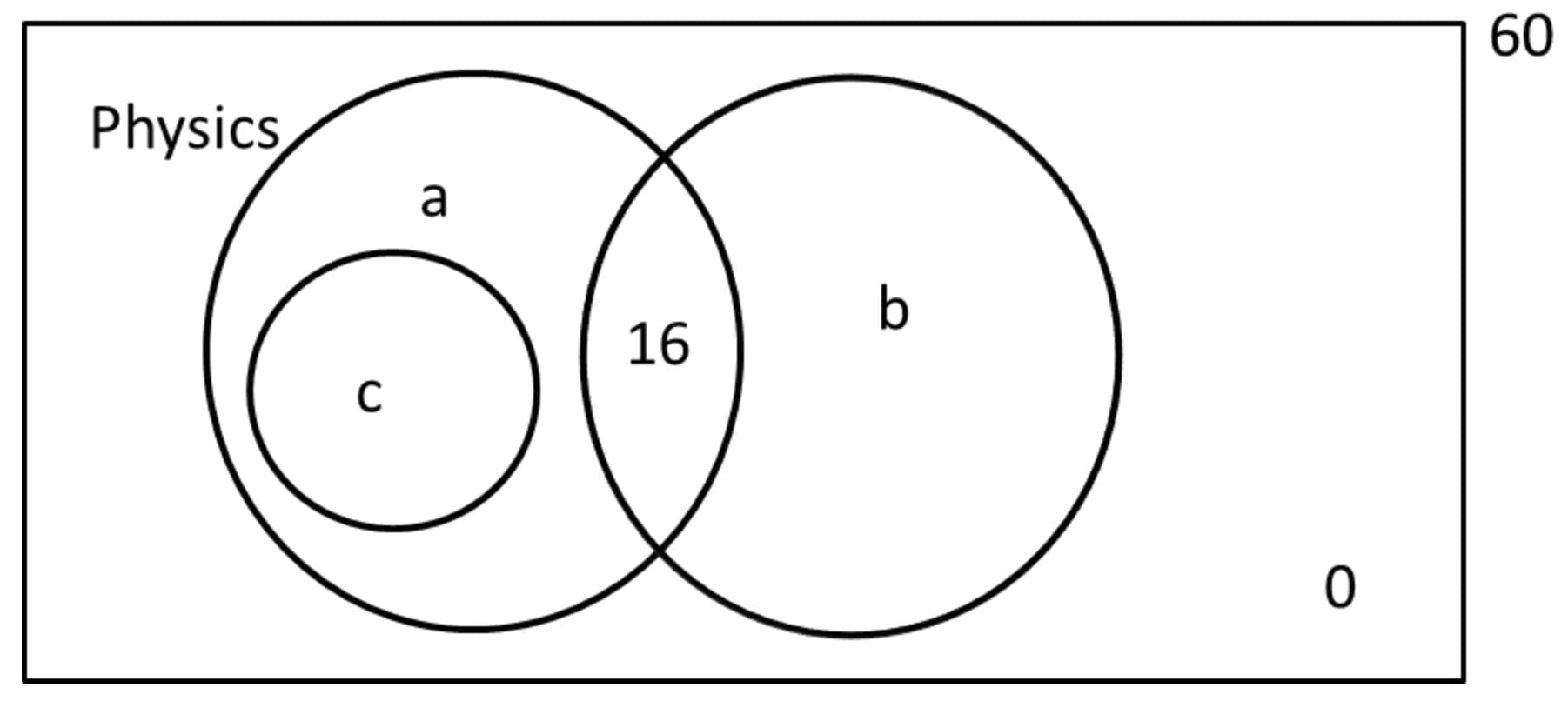
Of 60 students in a class, anyone who has chosen to study maths elects to do physics as well. But no one does maths and chemistry, 16 do physics and chemistry. All the students do at least one of the three subjects and the number of people who do exactly one of the three is more than the number who do more than one of the three. What are the maximum and minimum number of people who could have done Chemistry only?
Detailed Solution for Test: Venn Diagrams- 3 - Question 10

Anyone who does Maths does Physics also.

Maths is a subset of Physics. Now, let us build on this.
No one does maths and chemistry, 16 do physics and chemistry.

Number outside is 0 as all the students do at least one of the three subjects
a + b + c +16 = 60, or a + b + c = 44

The number of people who do exactly one of the three is more than the number who do more than one of the three. => a + b > c + 16
So, we have a + b + c = 44 and a + b > c + 16
We need to find the maximum and minimum possible values of b.
Let us start with the minimum. Let b = 0, a + c = 44. a > c + 16. We could have
a = 40, c = 4. So, b can be 0.
Now, thinking about the maximum value. b = 44, a = c = 0 also works.

So, minimum value = 0, maximum value = 44.

Hence, the answer is "44 and 0".
Choice D is the correct answer.

Information about Test: Venn Diagrams- 3 Page
In this test you can find the Exam questions for Test: Venn Diagrams- 3 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Venn Diagrams- 3, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for Venn Diagrams- 3

Find all the important questions for Venn Diagrams- 3 at EduRev.Get fully prepared for Venn Diagrams- 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Venn Diagrams- 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Venn Diagrams- 3 resources.

Venn Diagrams- 3 MCQs with Answers

Prepare for the Venn Diagrams- 3 within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Venn Diagrams- 3

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Venn Diagrams- 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily