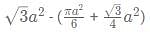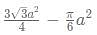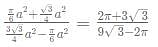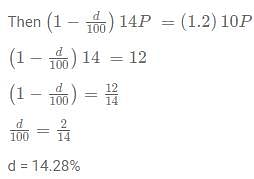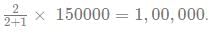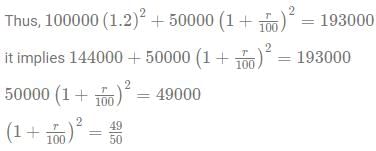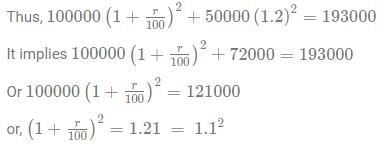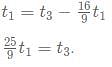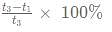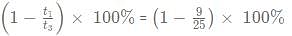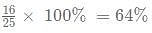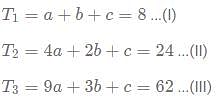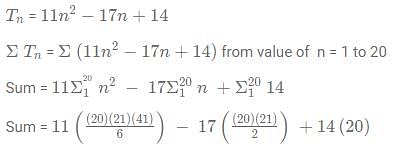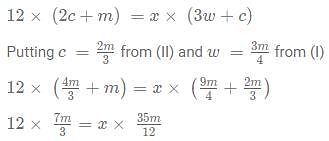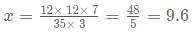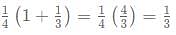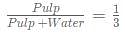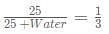CAT Mock Test- 7 (November 9) - CAT MCQ
30 Questions MCQ Test - CAT Mock Test- 7 (November 9)
In the third paragraph, why does the author remark that "ironically, the roles have reversed?"?
Which of the following could be an example of Weiner's desire-outcome disparity argument?
I. A weapons system, which cannot be stopped easily, starts bombing after receiving an erroneous command.
II. An AI program developed to mitigate global warming starts eliminating a fraction of the human population to complete its objective.
III. A Social media platform allows groups of militants to communicate their plans and coordinate their attacks.
I. A weapons system, which cannot be stopped easily, starts bombing after receiving an erroneous command.
II. An AI program developed to mitigate global warming starts eliminating a fraction of the human population to complete its objective.
III. A Social media platform allows groups of militants to communicate their plans and coordinate their attacks.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
All of the following have been discussed about gender equality in Sweden, EXCEPT:
Which of the following is likely to be the next course of discussion?
Which of the following cannot be inferred?
I. The effectiveness of 'big data' is determined not by its size but by its diversity.
II. Genes are a major factor influencing autism.
III. Consumption of a diet containing low levels of phenylalanine helps decrease the level of amino acid in the blood.
The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. On the contrary, the industry is happy reducing the wage bills, doing mechanisation and raising its profits.
2. During the pandemic, nearly 31 million families have moved down from the middle class and nearly 100 million people have lost jobs.
3. The industries that are most likely to create employment, i.e. the medium and small industries, are going down under and the large ones which do not create employment are the poster boys.
4. They are the ones that will get the 6 per cent productivity-linked incentive from the tax paid by the average taxpayers, with unknown consequences.
Five sentences related to a topic are given below. Four of them can be put together to form a meaningful and coherent short paragraph. Identify the odd one out.
1. Without robust national privacy safeguards, entire databases of citizen information are ready for purchase, whether to predatory loan companies, law enforcement agencies, or even malicious foreign actors.
2. Federal privacy bills that don’t give sufficient attention to data brokerage will therefore fail to tackle an enormous portion of the data surveillance economy.
3. Data brokerage is a threat to democracy.
4. This is why the largest data brokers are lobbying more aggressively in Washington.
5. This will leave civil rights, national security, and public-private boundaries vulnerable in the process.
The four sentences (labelled 1, 2, 3, and 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. However, the very ubiquity of such technology poses critical questions about data privacy and individual autonomy.
2. The integration of advanced algorithms and everyday technology has streamlined countless processes, improving efficiency exponentially.
3. As we entrust more of our lives to digital gatekeepers, the parameters of the debates shift from technical concerns to ethical dilemmas.
4. Such an environment, teeming with both subtle surveillance and convenience, highlights the double-edged nature of progress.
Directions: Read the question carefully and answer the question that follows:
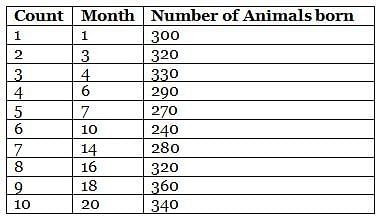
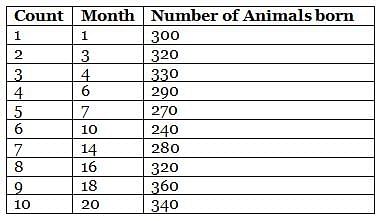
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. What is the average number of animals born between second count and third count that Mr. Wilson counted?
Directions: Read the question carefully and answer the question that follows:
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. What is the difference between the fifth count and the ninth count that Mr. Wilson took?
Directions: Read the question carefully and answer the question that follows:
Mr. Wilson works in a zoo, where he has to count the number of animals born in a month. He collates the data for the entire month at the end of the particular month. However, during a certain period of twenty months, from month 1 to month 20, Mr. Wilson counted the number of animals born on only ten months. He then plotted the ten points on a graph sheet and connected consecutive points on the graph using straight lines, forming a line graph.

Further, it is also known that
(1) the difference in number of animals born between any two consecutive counting that Mr. Wilson took was not more than 40
(2) the difference in the number of animals born counted by Mr. Wilson for the third time and for the fourth time was 40
(3) the second count that Mr. Wilson took was the same as the eighth count that he took.
Q. What is the average of the number of animals born during the ten months that Mr. Wilson counted?
Directions: Refer to the illustrations below and answer the question that follows.

Total units sold in 2014 = 2,52,000
Total units sold in 2015 = 3,24,000
Percent defective units of total units sold for each product:

Q. Of the total number of units sold in 2015, how many were defective?
Directions: Study the following information to answer the given question.
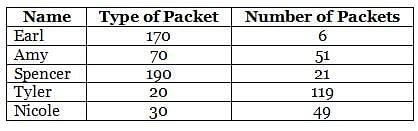
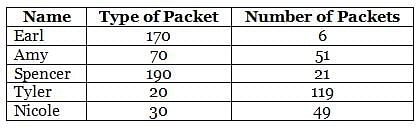
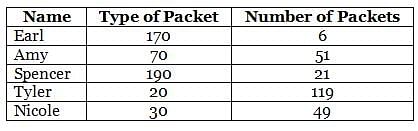
A certain candy manufacturing company manufactures candies and pack them in exactly five types of packets, which contain 20, 30, 70, 170 and 190 candies each. Each of five persons Earl, Amy, Spencer, Tyler and Nicole bought similar packing of candies and no two persons among the five bought same packing of candies. The numbers of candies that Earl, Amy, Spencer, Tyler and Nicole bought from the shopkeeper were 1020, 3570, 3990, 2380 and 1470, in that order. Further, the number of packets that each person bought from the shopkeeper was distinct. However, all of them realised that they had bought some extra candies, so they returned the excess candies in such a way that they made packets similar to those made by the company and each of Earl, Amy, Spencer, Tyler and Nicole returned in the form of 2 packets, 4 packets, 1 packet, 2 packets and 1 packet, respectively, but in packet(s) different from the type the person had bought from the shopkeeper.
Q. What is the total number of packets that the five persons bought from the shopkeeper?
Directions: Study the following information to answer the given question.
A certain candy manufacturing company manufactures candies and pack them in exactly five types of packets, which contain 20, 30, 70, 170 and 190 candies each. Each of five persons Earl, Amy, Spencer, Tyler and Nicole bought similar packing of candies and no two persons among the five bought same packing of candies. The numbers of candies that Earl, Amy, Spencer, Tyler and Nicole bought from the shopkeeper were 1020, 3570, 3990, 2380 and 1470, in that order. Further, the number of packets that each person bought from the shopkeeper was distinct. However, all of them realised that they had bought some extra candies, so they returned the excess candies in such a way that they made packets similar to those made by the company and each of Earl, Amy, Spencer, Tyler and Nicole returned in the form of 2 packets, 4 packets, 1 packet, 2 packets and 1 packet, respectively, but in packet(s) different from the type the person had bought from the shopkeeper.
Q. How many of the following statements are definitely true?
I. The number of packets that Earl purchased is an even number.
II. The number of packets that Amy purchased is an even number.
III. The number of packets that Spencer purchased is an odd number.
IV. The number of packets that Tyler purchased is an even number.
Directions: Study the following information to answer the given question.
A certain candy manufacturing company manufactures candies and pack them in exactly five types of packets, which contain 20, 30, 70, 170 and 190 candies each. Each of five persons Earl, Amy, Spencer, Tyler and Nicole bought similar packing of candies and no two persons among the five bought same packing of candies. The numbers of candies that Earl, Amy, Spencer, Tyler and Nicole bought from the shopkeeper were 1020, 3570, 3990, 2380 and 1470, in that order. Further, the number of packets that each person bought from the shopkeeper was distinct. However, all of them realised that they had bought some extra candies, so they returned the excess candies in such a way that they made packets similar to those made by the company and each of Earl, Amy, Spencer, Tyler and Nicole returned in the form of 2 packets, 4 packets, 1 packet, 2 packets and 1 packet, respectively, but in packet(s) different from the type the person had bought from the shopkeeper.
Q. Which of the following statements is correct?
Directions: Read the information given below and answer the question that follows.
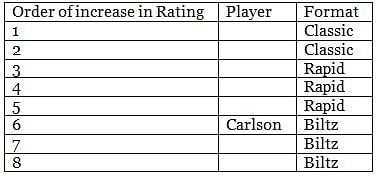
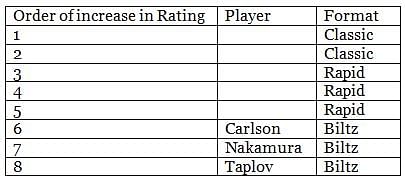
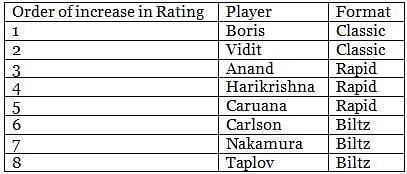
Eight chess players – Carlson, Caruana, Nakamura, Anand, Taplov, Vidit, Harikrishna and Boris – played three different format tournaments – Classic, Rapid and Biltz to increase their FIDE Ratings– such that each player played exactly one format. Two of the eight players played Classic, three played Rapid and three played Biltz. The increase in FIDE Ratings of each player is distinct. Further, the lowest increase in the rating in Classic format is higher than the highest increase in the rating in Rapid Format. Also the lowest increase in the rating in Rapid format is higher than the highest increase in the rating in Biltz Format.
It is also known that:
1. At least two players increased their ratings more than Anand's increase, and Anand did not increase his rating less than what Harikrishna did.
2. Vidit did not play Biltz and his increase of rating is just less than the increase of Boris.
3. Carlson got the highest increase in rating in Biltz.
4. Nakamura was not one with the lowest increase in his rating.
5. Caruana, who did not play Biltz, increased his rating less than what Harikrishna did.
Q. Who among the following was the player who got minimum increase in his rating?
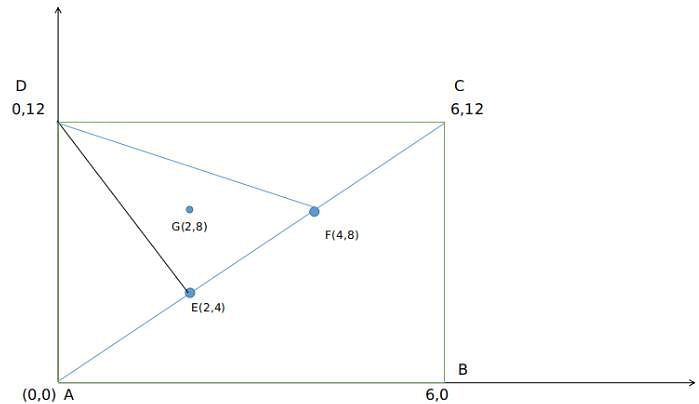
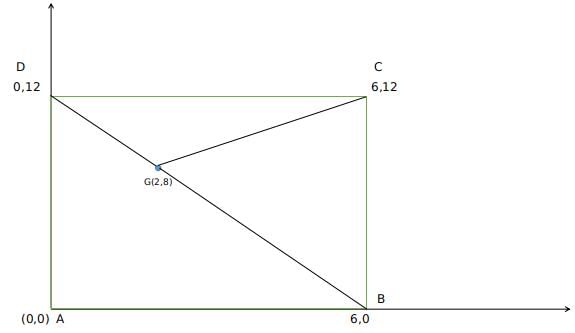
A rectangle ABCD exists such that AB = 6 units and BC = 12 units. E and F trisect the diagonal AC in 3 equal parts. G is centroid of the triangle formed by DEF. What is the area of DGBC?
How many 4-digit numbers exist which is divisible by 3 or 8?
What is the ratio of the shaded region to non-shaded region in the following diagram
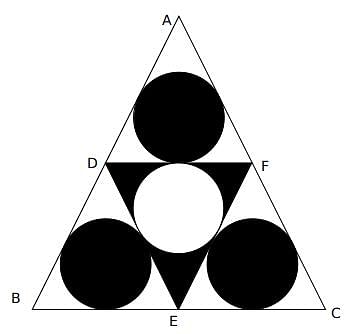
ABC is an equilateral triangle and D, E and F are the midpoint of the sides.
Siddhart is a pen-seller. He sells a pen such that the profit earned by selling 10 pens is equal to the cost price of 1 pen. The discount he gave on the marked price of the pen is 3 times the profit he earned by selling the pen. What approximate discount % should he offer the customer if he wishes to have a profit of 20%
A number N is given by = 25 x 38 x 42 x 53 x 6 x 72
If a certain factor of N is not divisible by 9, the probability that the factor is an odd number is m/n where 'n' is a natural number less than 20. Find the value of m+n.
Ram invests a total of Rs 1,50,000 into two schemes in the ratio 2:1. Both of the schemes have interest rates which are integers. After 2 years, Ram received a total of 1,93,000 in return. If one of the interest rates is 20%, and the interest rate of the other is R%, what is the value of R? Assume the interest to be compounded annually
A man was driving from city X to city Y. After travelling for 3 hours, his car develops a fault and his speed reduced to 1/3rd of his original speed. He was originally supposed to complete the journey in 17 hours. What was % increase in his overall travelling time?
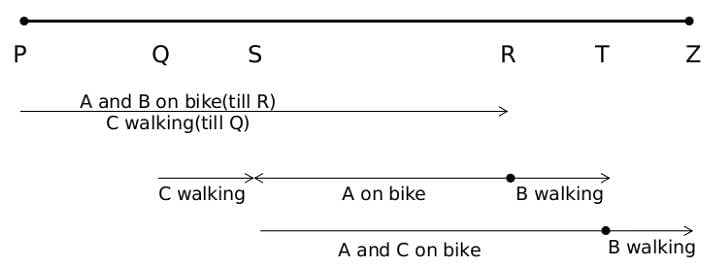
A, B and C are 3 friends who have to go to another city Z. A has a bike that has an average speed of 40 km/hr. B and C both can walk with an average speed of 5km/hr. To minimise the time taken for them to reach the other city it was decided that C will start walking towards the city Z while A will gives a lift to B for a certain distance after which A will drop-off B and B will start walking towards Z. A will go back to pick up C and then will start moving towards city Z. They all reach the destination at the same time. What percentage of the overall journey time, did B spend walking?
What is the sum of the first 20 numbers in the series 8,24,62,122, 204
2 men and a woman can complete a task in a certain number of days. If 13 men and 12 women work on the same task they can complete it in 1/8th of days required earlier. The number of days taken by 13 men and 12 women is equal to the number of days taken by 4 men and 27 children to finish the same task.
If 2 children and a man can complete another task in 12 days. What is the minimum number of days required by 3 women and 1 child to do the same task?
Even if they have to work for a fraction of a day, it will be counted as a whole day.
Fresh grapes have 75% water and the remaining 25% as fruit pulp. A shopkeeper bought a certain quantity of fresh grapes and let it dry so that the fraction of pulp in the grapes increase by 1/3rd of the original quantity. If the ratio of the evaporated water to the pulp is m:n where m and n are the lowest possible integers. Which of the following is the has maximum absolute value?
At how many points do the following curves C1 and C2 intersect?
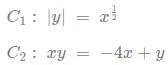


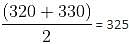
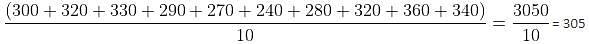
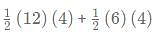
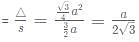
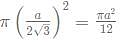
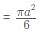
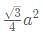
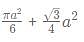
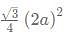 - Shaded area
- Shaded area