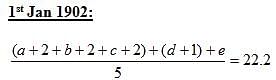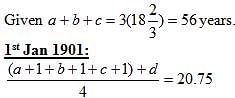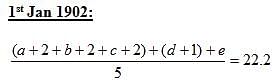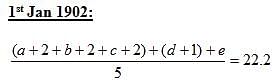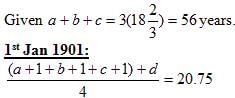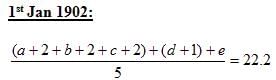CAT Mock Test - 17 (November 19) - CAT MCQ
30 Questions MCQ Test - CAT Mock Test - 17 (November 19)
Directions: Read the following passage carefully and answer the questions that follow.
Bill Gates is a lot luckier than you might realise. He may be a very talented man who worked his way up from geek to the top spot on the list of the world's richest people. But his extreme success perhaps tells us more about the importance of circumstances beyond his control than it does about how skill and perseverance are rewarded.
We often fall for the idea that the exceptional performers are the most skilled or talented. But this is flawed. Exceptional performances tend to occur in exceptional circumstances. Top performers are often the luckiest people, who have benefited from being at the right place and right time. They are what we call outliers, whose performances may be examples set apart from the system that everyone else works within.
Many treat Gates, and other highly successful people like him, as deserving of huge attention and reward, as people from whom we could learn a lot about how to succeed. But assuming life's "winners" got there from performance alone is likely to lead to disappointment. Even if you could imitate everything Gates did, you would not be able to replicate his initial good fortune.
For example, Gates's upper-class background and private education enabled him to gain extra programming experience when less than 0.01% of his generation then had access to computers. His mother's social connection with IBM's chairman enabled him to gain a contract from the then-leading PC company that was crucial for establishing his software empire.
This is important because most customers who used IBM computers were forced to learn how to use Microsoft's software that came along with it. This created an inertia in Microsoft's favour. The next software these customers chose was more likely to be Microsoft's, not because their software was necessarily the best, but because most people were too busy to learn how to use anything else.
Microsoft's success and market share may differ from the rest by several orders of magnitude, but the difference was really enabled by Gate's early fortune, reinforced by a strong success-breeds-success dynamic. Of course, Gates's talent and effort played important roles in the extreme success of Microsoft. But that's not enough for creating such an outlier. Talent and effort are likely to be less important than circumstances in the sense that he could not have been so successful without the latter.
One might argue that many exceptional performers still gained their exceptional skill through hard work, exceptional motivation or "grit", so they do not deserve to receive lower reward and praise. Some have even suggested that there is a magic number for greatness, a ten-year or 10,000-hour rule. Many professionals and experts did acquire their exceptional skill through persistent, deliberate practices. In fact, Gates' 10,000 hours learning computer programming as a teenager has been highlighted as one of the reasons for his success.
But detailed analyses of the case studies of experts often suggest that certain situational factors beyond the control of these exceptional performers also play an important role. For example, three national champions in table tennis came from the same street in a small suburb of one town in England.
This wasn't a coincidence or because there was nothing else to do but practise ping pong. It turns out that a famous table tennis coach, Peter Charters, happened to retire in this particular suburb. Many kids who lived on the same street as the retired coach were attracted to this sport because of him and three of them, after following the "10,000-hour rule", performed exceptionally well, including winning the national championship.
Their talent and efforts were, of course, essential for realising their exceptional performances. But without their early luck (having a reliable, high-quality coach and supportive families), simply practicing 10,000 hours without adequate feedback wouldn't likely lead a randomly picked child to become a national champion.
We could also imagine a child with superior talent in table tennis suffering from early bad luck, such as not having a capable coach or being in a country where being an athlete was not considered to be a promising career. Then they might never have a chance to realise their potential. The implication is that the more exceptional a performance is, the fewer meaningful, applicable lessons we can actually learn from the "winner".
When it comes to moderate performance, it seems much more likely that our intuition about success is correct. Conventional wisdom, such as "the harder I work the luckier I get" or "chance favours the prepared mind", makes perfect sense when talking about someone moving from poor to good performance. Going from good to great, however, is a different story.
Being in the right place (succeeding in a context where early outcome has an enduring impact) at the right time (having early luck) can be so important that it overwhelms merits. With this in mind there's a good case that we shouldn't just reward or imitate life's winners and expect to have similar success. But there is a case that the winners should consider imitating the likes of Gates (who became a philanthropist) or Warren Buffett (who argues that richer Americans should pay higher taxes) who have chosen to use their wealth and success to do good things. The winners who appreciate their luck and do not take it all deserve more of our respect.
Q. Which of the following examples best represent an outlier, as described in the passage?
Directions: Read the following passage carefully and answer the questions that follow.
Bill Gates is a lot luckier than you might realise. He may be a very talented man who worked his way up from geek to the top spot on the list of the world's richest people. But his extreme success perhaps tells us more about the importance of circumstances beyond his control than it does about how skill and perseverance are rewarded.
We often fall for the idea that the exceptional performers are the most skilled or talented. But this is flawed. Exceptional performances tend to occur in exceptional circumstances. Top performers are often the luckiest people, who have benefited from being at the right place and right time. They are what we call outliers, whose performances may be examples set apart from the system that everyone else works within.
Many treat Gates, and other highly successful people like him, as deserving of huge attention and reward, as people from whom we could learn a lot about how to succeed. But assuming life's "winners" got there from performance alone is likely to lead to disappointment. Even if you could imitate everything Gates did, you would not be able to replicate his initial good fortune.
For example, Gates's upper-class background and private education enabled him to gain extra programming experience when less than 0.01% of his generation then had access to computers. His mother's social connection with IBM's chairman enabled him to gain a contract from the then-leading PC company that was crucial for establishing his software empire.
This is important because most customers who used IBM computers were forced to learn how to use Microsoft's software that came along with it. This created an inertia in Microsoft's favour. The next software these customers chose was more likely to be Microsoft's, not because their software was necessarily the best, but because most people were too busy to learn how to use anything else.
Microsoft's success and market share may differ from the rest by several orders of magnitude, but the difference was really enabled by Gate's early fortune, reinforced by a strong success-breeds-success dynamic. Of course, Gates's talent and effort played important roles in the extreme success of Microsoft. But that's not enough for creating such an outlier. Talent and effort are likely to be less important than circumstances in the sense that he could not have been so successful without the latter.
One might argue that many exceptional performers still gained their exceptional skill through hard work, exceptional motivation or "grit", so they do not deserve to receive lower reward and praise. Some have even suggested that there is a magic number for greatness, a ten-year or 10,000-hour rule. Many professionals and experts did acquire their exceptional skill through persistent, deliberate practices. In fact, Gates' 10,000 hours learning computer programming as a teenager has been highlighted as one of the reasons for his success.
But detailed analyses of the case studies of experts often suggest that certain situational factors beyond the control of these exceptional performers also play an important role. For example, three national champions in table tennis came from the same street in a small suburb of one town in England.
This wasn't a coincidence or because there was nothing else to do but practise ping pong. It turns out that a famous table tennis coach, Peter Charters, happened to retire in this particular suburb. Many kids who lived on the same street as the retired coach were attracted to this sport because of him and three of them, after following the "10,000-hour rule", performed exceptionally well, including winning the national championship.
Their talent and efforts were, of course, essential for realising their exceptional performances. But without their early luck (having a reliable, high-quality coach and supportive families), simply practicing 10,000 hours without adequate feedback wouldn't likely lead a randomly picked child to become a national champion.
We could also imagine a child with superior talent in table tennis suffering from early bad luck, such as not having a capable coach or being in a country where being an athlete was not considered to be a promising career. Then they might never have a chance to realise their potential. The implication is that the more exceptional a performance is, the fewer meaningful, applicable lessons we can actually learn from the "winner".
When it comes to moderate performance, it seems much more likely that our intuition about success is correct. Conventional wisdom, such as "the harder I work the luckier I get" or "chance favours the prepared mind", makes perfect sense when talking about someone moving from poor to good performance. Going from good to great, however, is a different story.
Being in the right place (succeeding in a context where early outcome has an enduring impact) at the right time (having early luck) can be so important that it overwhelms merits. With this in mind there's a good case that we shouldn't just reward or imitate life's winners and expect to have similar success. But there is a case that the winners should consider imitating the likes of Gates (who became a philanthropist) or Warren Buffett (who argues that richer Americans should pay higher taxes) who have chosen to use their wealth and success to do good things. The winners who appreciate their luck and do not take it all deserve more of our respect.
Q. It can be understood that the main purpose of the author in the third paragraph is to:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: Read the following passage carefully and answer the questions that follow.
After many years of practising Buddhism in Thailand, my experience expands beyond the immediate community in Sri Racha. In recent years as I have visited the White Dragon Temple, the social unrest in Thailand has crept into the religious aspect of my trips.
Religion exists as an innate piece of the landscape that etches itself into the small details of Thailand. It occupies both a very physical presence within the community and also a mental one. According to the Office of National Buddhism, 40,717 Buddhist temples exist in Thailand. Of these temples, a large portion resides in Bangkok, Thailand's capital.
Aside from being an important tourist element, Buddhism plays an important part in the lives of Thai people - an estimated 94% of all Thai people practice Buddhism in the country according to a Central Intelligence Agency report. Time and time again, there have been movements - in 1997, 2007, and 2014 - to concretize Buddhism as the nation's official religion. The Thai Constitutional Drafting Committee (CDC) has, however, remained neutral in the relationship between the state and religion.
Though the government's ideological stance on religion is decidedly impartial, significant ripples exist in this seemingly placid surface, and religion morphs into a central focal point in many instances, whether the Thai government takes an intimate position on it or not. Faith remains a link to the personal lives of common citizens and royalty alike. King Bhumibol's funeral on October 14, 2016 featured traditional Buddhist funeral rites with the ritualistic bathing of the king's body and the chanting of orange-robed monks. Adding to this ceremonious burial, his body resided in the Temple of the Emerald Buddha so that people could pay their respects to the revered king, who provided stability for his country for 70 years. Though the king in Thailand did not hold any true, legislative power, he was a reverential symbol for the people of the country. His majesty's death occurred at a moment of tension in the country as a number of attacks rocked Thailand and has only caused this pressure to spill-over. Religion is something that connects people in Thailand yet, at the same time, can be a divisive element as is evident from attacks that have occurred in the nation over the last few years.
In the span of less than a day between August 11th and 12th of 2016, 11 bombings hit five provinces in Thailand, killing at least four Thai nationals and injuring 36. These bombings occurred almost a year after one of the most devastating attacks in Thai history in Bangkok, which killed 20 people and wounded 125 more. What's more, these attacks coincided with the Queen Sirikit's birthday. On August 17, 2015, Uighur militants splintered the Thai state as they bombed the Erawan Shrine. Though the motives for the attack were more aimed at the states' repatriation of Uighur refugees, the targeting of the temple was calculated: not only is the area around the shrine a densely populated area but also, it is frequented by many tourists. These acts of terrorism that assail the kingdom have left many Thais scared and unsure in a time, without a unifying leader. Known epithetically as the "land of smiles," Thailand has had little to smile about of late.
In light of this tumultuous time in the nation's history, religious institutions like the White Dragon Temple became integral in steadying the country's course. Through the diligent service that the temple provides for the community, it is a rallying point for many frightened Thais. See Knok, the central spiritual leader in the temple, and his followers have proved to be a "stabilizing element in the wake of the King's death," especially in Sri Racha, by continuing with their public works projects - providing educational help, burial services, food distribution, and a variety of other support structures. These actions from local community leaders have started to mend the fractures that occur on a national level.
I returned to Thailand in August of 2016, during the bombings in the southern provinces of the country. On one day during this visit, I bagged fruit and food for followers and local community members alike. The cadence of shifting palates of food and thump of vegetables into bags kept time with my human tempo. With each bag I loaded onto the palates, I could measure the burden on the community of Sri Racha lift slightly. In the glimmering eyes of the young men that I worked with, I could see the brightness of Thailand's future. Beneath me, I could feel the flexing and contracting of a nation, not torn by conflict but ready to rebuild and strive onward if only for a moment.
Q. What is the main purpose behind the author's words when he says: "Known epithetically as the "land of smiles," Thailand has had little to smile about of late"?
Directions: Read the following passage carefully and answer the questions that follow.
No language has spread as widely as English, and it continues to spread. Internationally the desire to learn it is insatiable. In the twenty-first century the world is becoming more urban and more middle class, and the adoption of English is a symptom of this, for increasingly English serves as the lingua franca of business and popular culture. It is dominant or at least very prominent in other areas such as shipping, diplomacy, computing, medicine and education. A recent study has suggested that among students in the United Arab Emirates "Arabic is associated with tradition, home, religion, culture, school, arts and social sciences," whereas English "is symbolic of modernity, respect, work, higher education, commerce, economics and science and technology."
Wherever English has been used, it has lasted. Cultural might outlives military rule. In the colonial period, the languages of settlers dominated the languages of the peoples whose land they seized. They marginalized them and in some cases eventually drove them to extinction. All the while they absorbed from them whatever local terms seemed useful. The colonists' languages practised a sort of cannibalism, and its legacy is still sharply felt. English is treated with suspicion in many places where it was once the language of the imperial overlords. It is far from being a force for unity, and its endurance is stressful. In India, while English is much used in the media, administration, education and business, there are calls to curb its influence. Yet even where English has been denigrated as an instrument of colonialism, it has held on - and in most cases grown, increasing its numbers of speakers and functions.
Today it is English, rather than any created alternative, that is the world's auxiliary tongue. There are more people who use English as a second language than there are native speakers. Estimates of the numbers vary, but even the most guarded view is that English has 500 million second-language speakers. Far more of the world's citizens are eagerly jumping on board than trying to resist its progress. In places where English is used as a second language, its users often perceive it as free from the limitations of their native languages. They associate it with power and social status, and see it as a supple and sensuous medium for self-expression. It symbolizes choice and liberty. But while many of those who do not have a grasp of the language aspire to learn it, there are many others who perceive it as an instrument of oppression, associated not only with imperialism but also with the predations of capitalism and Christianity.
There are challenges to the position of English as the dominant world language in the twenty-first century. The main ones seem likely to come from Spanish and Mandarin Chinese. Both have more first-language users than English. But at present neither is much used as a lingua franca. The majority of speakers of Mandarin Chinese live in one country, and, excepting Spain, most Spanish-speakers are in the Americas. Two challenges stand out. I have mentioned India already; English is important to its global ambitions. The language's roots there are colonial, but English connects Indians less to the past than to the future. Already the language is used by more people in India than in any other country, the United States included. Meanwhile in China the number of students learning the language is increasing rapidly. The entrepreneur Li Yang has developed Crazy English, an unorthodox teaching method. It involves a lot of shouting. This, Li explains, is the way for Chinese to activate their "international muscles." His agenda is patriotic.
The embrace of English in the world's two most populous countries means that the language is changing. Some of the changes are likely to prove disconcerting for its native speakers. The "English-ness" of English is being diluted. So, more surprisingly, is its American flavour. English's centre of gravity is moving; in fact, in the twenty-first century the language has many centres. As this continues, native English-speakers may find themselves at a disadvantage.
At the same time, native speakers of English tend to assume that their ability in this potent language makes it unimportant to learn other languages. The reality is different. British companies often miss out on export opportunities because of a lack of relevant language skills. Moreover, there is a chance that a command of English will within twenty or thirty years be regarded as a basic skill for business, and native speakers of the language will no longer enjoy any competitive advantage. The consequences are complex. Some, it would seem, are not as intended. Even as vast amounts are spent on spreading British English, the reality is that English is taking on more and more local colour in the different places where it is used. Accordingly, while the number of languages in the world is diminishing, the number of Englishes is increasing.
Q. It can be understood from the context of the passage that when the author says: "the number of Englishes is increasing", he means which of the following?
Passage: In all battles two things are usually required of the Commander—in—Chief: to make a good plan for his army and to keep a strong reserve. Both of these are also obligatory for the painter. To make a plan, thorough reconnaissance of the country where the battle is to be fought is needed. Its fields, its mountains, its rivers, its bridges, its trees, its flowers, its atmosphere—all require and repay attentive observation from a special point of view. I think this is one of the chief delights that have come to me through painting. No doubt many people who are lovers of art have acquired it to a high degree without actually practicing.
But I expect that nothing will make one observe more quickly or more thoroughly than having to face the difficulty of representing the thing observed. And mind you, if you do observe accurately and with refinement, and if you do record what you have seen with tolerable correspondence, the result follows on the canvas with startling obedience. But in order to make his plan, the General must not only reconnoiter the battle—ground; he must also study the achievements of the great Captains of the past. He must bring the observations he has collected in the field into comparison with the treatment of similar incidents by famous chiefs. Considering that, the galleries of Europe take on a new—and to me at least a severely practical—interest. "This, then, is how —— painted a cataract.
Exactly, and there is that same light I noticed last week in the waterfall at ——. " And so on. You see the difficulty that baffled you yesterday; and you see how easily it has been overcome by a great or even by a skillful painter. Not only is your observation of Nature sensibly improved and developed, but also your comprehension of the masterpieces of art. But it is in the use and withholding of their reserves that the great commanders have generally excelled. After all, when once the last reserve has been thrown in, the commander's part is played.
If that does not win the battle, he has nothing else to give. Everything must be left to luck and to the fighting troops. But these last reserves, in the absence of high direction, are apt to get into sad confusion, all mixed together in a nasty mess, without order or plan—and consequently without effect. Mere masses count no more. The largest brush, the brightest colors cannot even make an impression. The pictorial battlefield becomes a sea of mud mercifully veiled by the fog of war. Even though the General plunges in himself and emerges bespattered, as he sometimes does, he will not retrieve the day. In painting, the reserves consist in Proportion or Relation.
And it is here that the art of the painter marches along the road which is traversed by all the greatest harmonies in thought. At one side of the palette there is white, at the other black; and neither is ever used ?neat.' Between these two rigid limits all the action must lie, all the power required must be generated. Black and white themselves placed in juxtaposition make no great impression; and yet they are the most that you can do in pure contrast.
Q. Below are listed various opinions that might possibly be ascribed to the author. Based on the passage, which of the following could most reasonably be attributed to the author?
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
As Soviet power declined, the world became to some extent multipolar, and Europe strove to define an independent identity. What a journey Europe has undertaken to reach this point. It had in every century changed its internal structure and invented new ways of thinking about the nature of international order. Now at the culmination of an era, Europe, in order to participate in it, felt obliged to set aside the political mechanisms through which it had conducted its affairs for three and a half centuries. Impelled also by the desire to cushion the emergent unification of Germany, the new European Union established a common currency in 2002 and a formal political structure in 2004. It proclaimed a Europe united, whole, and free, adjusting its differences by peaceful mechanisms.
Directions: Read the information given below and answer the question that follows.
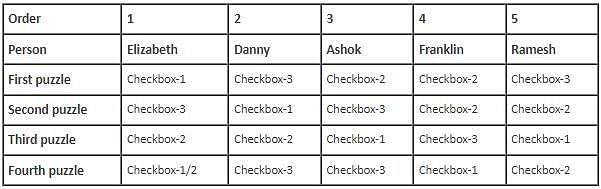
Five contestants, Danny, Elizabeth, Ashok, Ramesh and Franklin, entered in a puzzle show which had four puzzles – First puzzle, Second puzzle, Third puzzle and Fourth puzzle. Each puzzle had three checkboxes, Checkbox-1, Checkbox-2 and Checkbox-3, and each contestant had to choose one of the three checkboxes as his/her answer for each. The five contestants were sitting in a line, one behind the other, facing the same direction, not necessarily in the same order as mentioned above. During the show, except for the contestant sitting at the beginning of the line, each contestant copied the answer to exactly one puzzle from the contestant immediately in front of him. Further, for any pair of contestants sitting immediately next to each other, exactly one answer was the same (i.e. the answer that was copied).
It is also known that:
(i) The contestant sitting at the last position, who was not Ashok, marked the answer as Checkbox-2 for Second puzzle and Franklin, who was not at the last position, did not mark the answer to Third puzzle as Checkbox-2.
(ii) Exactly two contestants marked the answer as Checkbox-2 for First puzzle and neither of the two was sitting at any of the ends.
(iii) Danny, who was sitting immediately in front of Ashok, marked the answer as Checkbox-3 for exactly two puzzles, while Ramesh marked the answer as Checkbox-3 only for First puzzle.
(iv) Each of the four contestants who copied the answer did so for a different puzzle and each contestant marked the answer as Checkbox-1 for at least one puzzle, as Checkbox-2 for at least one puzzle and as Checkbox-3 for at least one puzzle.
(v) The contestant sitting in the middle marked the answer to Second puzzle as Checkbox-3, which he did not copy.
(vi) The contestant sitting at the second position, who was not Ashok, marked the answer as Checkbox-2 for Third puzzle, which he copied.
Q. What is the answer marked for Fourth puzzle by the contestant sitting in the last position?
Directions: Read the information given below and answer the question that follows.
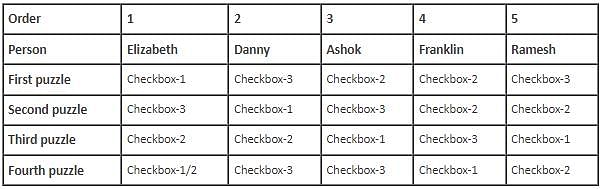
Five contestants, Danny, Elizabeth, Ashok, Ramesh and Franklin, entered in a puzzle show which had four puzzles – First puzzle, Second puzzle, Third puzzle and Fourth puzzle. Each puzzle had three checkboxes, Checkbox-1, Checkbox-2 and Checkbox-3, and each contestant had to choose one of the three checkboxes as his/her answer for each. The five contestants were sitting in a line, one behind the other, facing the same direction, not necessarily in the same order as mentioned above. During the show, except for the contestant sitting at the beginning of the line, each contestant copied the answer to exactly one puzzle from the contestant immediately in front of him. Further, for any pair of contestants sitting immediately next to each other, exactly one answer was the same (i.e. the answer that was copied).
It is also known that:
(i) The contestant sitting at the last position, who was not Ashok, marked the answer as Checkbox-2 for Second puzzle and Franklin, who was not at the last position, did not mark the answer to Third puzzle as Checkbox-2.
(ii) Exactly two contestants marked the answer as Checkbox-2 for First puzzle and neither of the two was sitting at any of the ends.
(iii) Danny, who was sitting immediately in front of Ashok, marked the answer as Checkbox-3 for exactly two puzzles, while Ramesh marked the answer as Checkbox-3 only for First puzzle.
(iv) Each of the four contestants who copied the answer did so for a different puzzle and each contestant marked the answer as Checkbox-1 for at least one puzzle, as Checkbox-2 for at least one puzzle and as Checkbox-3 for at least one puzzle.
(v) The contestant sitting in the middle marked the answer to Second puzzle as Checkbox-3, which he did not copy.
(vi) The contestant sitting at the second position, who was not Ashok, marked the answer as Checkbox-2 for Third puzzle, which he copied.
Q. Which checkbox was marked by the maximum number of contestants for Fourth puzzle?
Directions: Read the information given below and answer the question that follows.
Five contestants, Danny, Elizabeth, Ashok, Ramesh and Franklin, entered in a puzzle show which had four puzzles – First puzzle, Second puzzle, Third puzzle and Fourth puzzle. Each puzzle had three checkboxes, Checkbox-1, Checkbox-2 and Checkbox-3, and each contestant had to choose one of the three checkboxes as his/her answer for each. The five contestants were sitting in a line, one behind the other, facing the same direction, not necessarily in the same order as mentioned above. During the show, except for the contestant sitting at the beginning of the line, each contestant copied the answer to exactly one puzzle from the contestant immediately in front of him. Further, for any pair of contestants sitting immediately next to each other, exactly one answer was the same (i.e. the answer that was copied).
It is also known that:
(i) The contestant sitting at the last position, who was not Ashok, marked the answer as Checkbox-2 for Second puzzle and Franklin, who was not at the last position, did not mark the answer to Third puzzle as Checkbox-2.
(ii) Exactly two contestants marked the answer as Checkbox-2 for First puzzle and neither of the two was sitting at any of the ends.
(iii) Danny, who was sitting immediately in front of Ashok, marked the answer as Checkbox-3 for exactly two puzzles, while Ramesh marked the answer as Checkbox-3 only for First puzzle.
(iv) Each of the four contestants who copied the answer did so for a different puzzle and each contestant marked the answer as Checkbox-1 for at least one puzzle, as Checkbox-2 for at least one puzzle and as Checkbox-3 for at least one puzzle.
(v) The contestant sitting in the middle marked the answer to Second puzzle as Checkbox-3, which he did not copy.
(vi) The contestant sitting at the second position, who was not Ashok, marked the answer as Checkbox-2 for Third puzzle, which he copied.
Q. Who among the following marked the answer to First puzzle as Checkbox-1?
Directions: Read the following and answer the question that follows.
Indra Co-operative Society began with a membership of three members on 1st January, 1900. The average age of this group was 18 2/3 years. Every year, a new member joined this society. The age of the individual person on 1st January of any year is an integer. The average age of the group as on 1st January, 1901 and on 1st January, 1902 was 20.75 years and 22.2 years, respectively. At any instance, the ages (in years) of the members of the group are all distinct. The eldest person in the group (of the five members) as on 1st January, 1902 was of 25 years of age. The age of any member cannot be less than 17 years on 1st January, 1900.
Q. If the eldest person among the ones, who first became members of the Indra Co-operative Society was only one year older than the other member, what was his age in years?
Directions: Read the following and answer the question that follows.
Indra Co-operative Society began with a membership of three members on 1st January, 1900. The average age of this group was 18 2/3 years. Every year, a new member joined this society. The age of the individual person on 1st January of any year is an integer. The average age of the group as on 1st January, 1901 and on 1st January, 1902 was 20.75 years and 22.2 years, respectively. At any instance, the ages (in years) of the members of the group are all distinct. The eldest person in the group (of the five members) as on 1st January, 1902 was of 25 years of age. The age of any member cannot be less than 17 years on 1st January, 1900.
Q. What was the age (as on 1st January, 1902), in years, of the member who joined the group on 1st January, 1902?
Directions: Read the following and answer the question that follows.
Indra Co-operative Society began with a membership of three members on 1st January, 1900. The average age of this group was 18 2/3 years. Every year, a new member joined this society. The age of the individual person on 1st January of any year is an integer. The average age of the group as on 1st January, 1901 and on 1st January, 1902 was 20.75 years and 22.2 years, respectively. At any instance, the ages (in years) of the members of the group are all distinct. The eldest person in the group (of the five members) as on 1st January, 1902 was of 25 years of age. The age of any member cannot be less than 17 years on 1st January, 1900.
Q. What can be the maximum possible difference, in years, between the ages of the second eldest and the second youngest as on 1st January, 1902?
Directions: Read the following and answer the question that follows.
Indra Co-operative Society began with a membership of three members on 1st January, 1900. The average age of this group was 18 2/3 years. Every year, a new member joined this society. The age of the individual person on 1st January of any year is an integer. The average age of the group as on 1st January, 1901 and on 1st January, 1902 was 20.75 years and 22.2 years, respectively. At any instance, the ages (in years) of the members of the group are all distinct. The eldest person in the group (of the five members) as on 1st January, 1902 was of 25 years of age. The age of any member cannot be less than 17 years on 1st January, 1900.
Q. As on 1st January, 1902, the median age of the five members of the society is
Directions: Read the information given below and answer the question that follows.
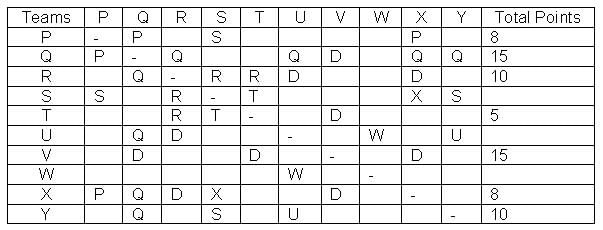
In a Kabaddi tournament ten teams P, Q, R, S, T, U, V, W, X and Y participated wherein every team played exactly one match with every other team. The result of the matches between the teams are given in incomplete table. The points awarded to a team for a win, draw and a loss are +2, +1 and 0 respectively. The team with the highest number of points at the end is the winner of the tournament.
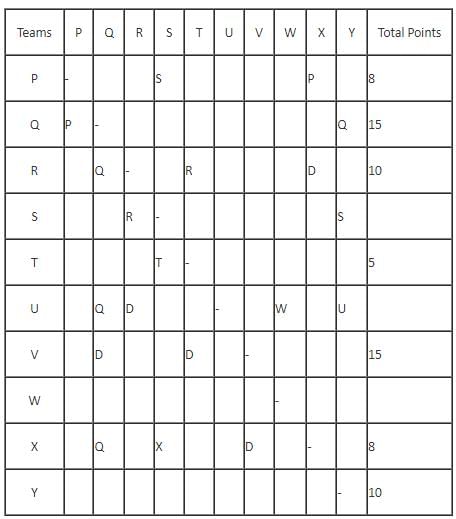
The entry in any particular cell of the table gives the winner of the match between the corresponding two teams, unless the cell contains 'Draw' which means the match ended in a draw. The following information is also available:
(1) The team which got maximum points lost at most 1 match.
(2) The total number of points of R is greater than that of U.
(3) Only five matches ended as a draw.
(4) W lost all matches except one.
Q. The match between which of the following teams ended in a draw?
Directions: Read the information given below and answer the question that follows.
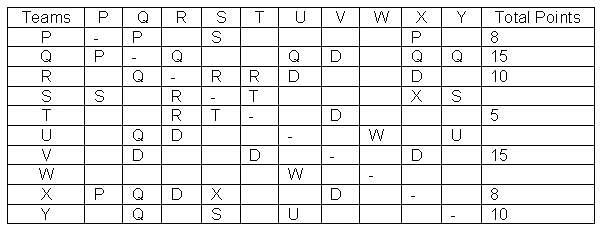
In a Kabaddi tournament ten teams P, Q, R, S, T, U, V, W, X and Y participated wherein every team played exactly one match with every other team. The result of the matches between the teams are given in incomplete table. The points awarded to a team for a win, draw and a loss are +2, +1 and 0 respectively. The team with the highest number of points at the end is the winner of the tournament.
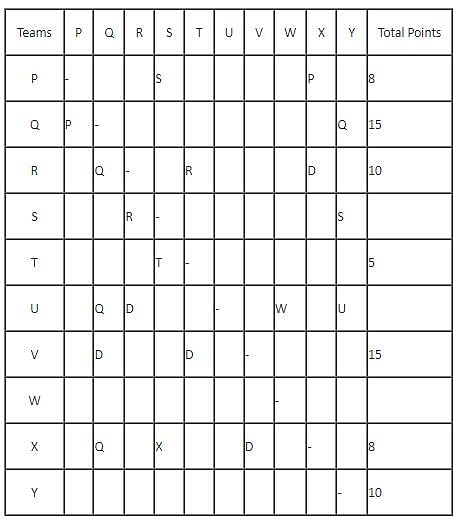
The entry in any particular cell of the table gives the winner of the match between the corresponding two teams, unless the cell contains 'Draw' which means the match ended in a draw. The following information is also available:
(1) The team which got maximum points lost at most 1 match.
(2) The total number of points of R is greater than that of U.
(3) Only five matches ended as a draw.
(4) W lost all matches except one.
Q. What is the difference between maximum number of points scored by any team and the minimum number of points scored by any team?
Directions: Read the information given below and answer the question that follows.
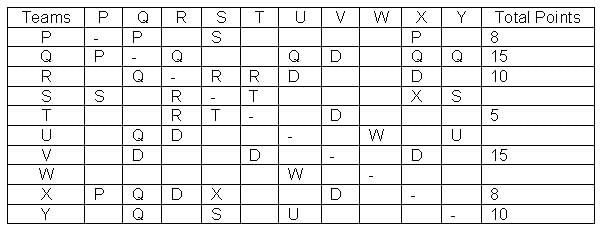
In a Kabaddi tournament ten teams P, Q, R, S, T, U, V, W, X and Y participated wherein every team played exactly one match with every other team. The result of the matches between the teams are given in incomplete table. The points awarded to a team for a win, draw and a loss are +2, +1 and 0 respectively. The team with the highest number of points at the end is the winner of the tournament.
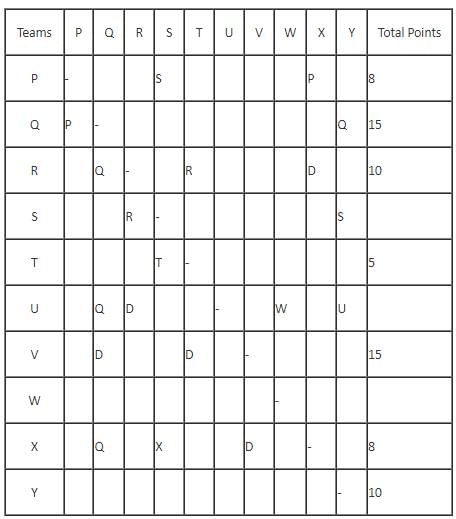
The entry in any particular cell of the table gives the winner of the match between the corresponding two teams, unless the cell contains 'Draw' which means the match ended in a draw. The following information is also available:
(1) The team which got maximum points lost at most 1 match.
(2) The total number of points of R is greater than that of U.
(3) Only five matches ended as a draw.
(4) W lost all matches except one.
Q. Which of the following statements is definitely true?
Directions: Read the information given below and answer the question that follows.
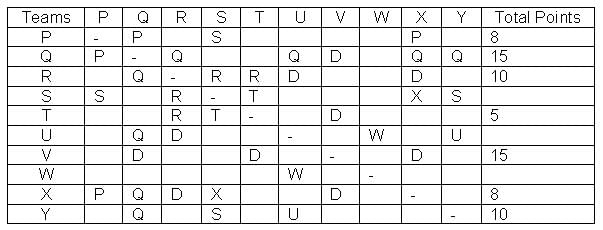
In a Kabaddi tournament ten teams P, Q, R, S, T, U, V, W, X and Y participated wherein every team played exactly one match with every other team. The result of the matches between the teams are given in incomplete table. The points awarded to a team for a win, draw and a loss are +2, +1 and 0 respectively. The team with the highest number of points at the end is the winner of the tournament.
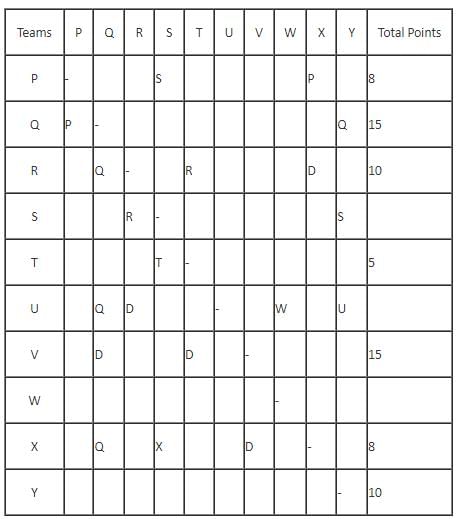
The entry in any particular cell of the table gives the winner of the match between the corresponding two teams, unless the cell contains 'Draw' which means the match ended in a draw. The following information is also available:
(1) The team which got maximum points lost at most 1 match.
(2) The total number of points of R is greater than that of U.
(3) Only five matches ended as a draw.
(4) W lost all matches except one.
Q. The maximum matches of which team ended in a draw?
Directions: Study the following information and answer the question.
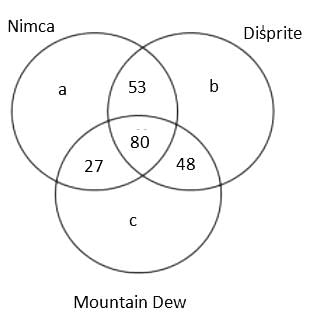
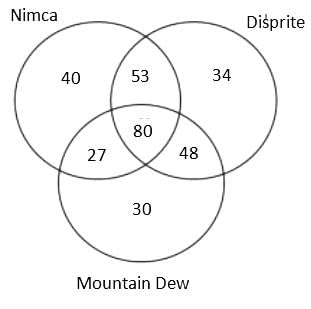
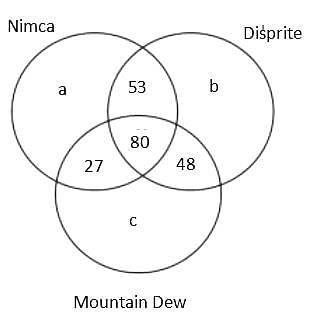
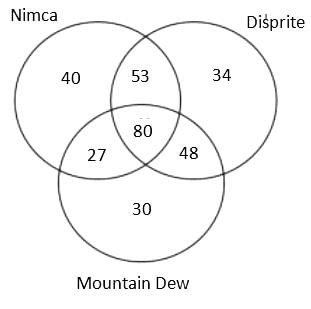
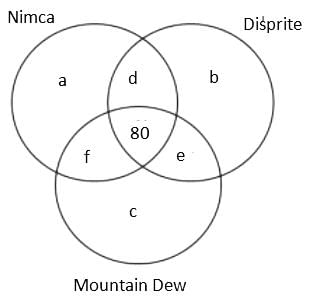
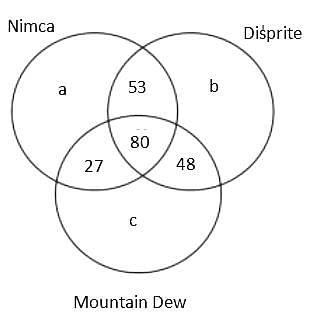
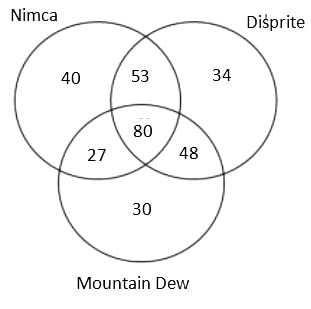
A Patna based consulting firm was celebrating the success, so they organised a party for employees. In the party, total 3 types of cold drink were served, namely, Nimca, Disprite and Mountain Dew. It is known that total 400 members were present there but 22% members didn't drink any of the three types of cold drink. Further, it is known that total 600 bottles were served in the party.
The additional information is given below:
(1) The number of employees who drank both Nimca and Disprite was 5 more than the number of employees who drank both Disprite and Mountain Dew.
(2) The sum of the number of employees who drank Nimca and Disprite only and who drank Nimca and Mountain Dew only was equal to the number of employees who drank all the three types of cold drink
(3) The ratio of the total number of bottles of Mountain Dew to the total number of bottles of Disprite served was 37 : 43.
(4) The cold drinks were served in bottles only and no employee drank more than one bottle of the same type of cold drink.
(5) The number of employees who drank all the three types of cold drink was 80.
Q. How many employees drank only one bottle of any type of cold drink?
Directions: Study the following information and answer the question.
A Patna based consulting firm was celebrating the success, so they organised a party for employees. In the party, total 3 types of cold drink were served, namely, Nimca, Disprite and Mountain Dew. It is known that total 400 members were present there but 22% members didn't drink any of the three types of cold drink. Further, it is known that total 600 bottles were served in the party.
The additional information is given below:
(1) The number of employees who drank both Nimca and Disprite was 5 more than the number of employees who drank both Disprite and Mountain Dew.
(2) The sum of the number of employees who drank Nimca and Disprite only and who drank Nimca and Mountain Dew only was equal to the number of employees who drank all the three types of cold drink
(3) The ratio of the total number of bottles of Mountain Dew to the total number of bottles of Disprite served was 37 : 43.
(4) The cold drinks were served in bottles only and no employee drank more than one bottle of the same type of cold drink.
(5) The number of employees who drank all the three types of cold drink was 80.
Q. If X is the number of employees who drank exactly two bottles, then what is the sum of all the factors of X?
Directions: Study the following information and answer the question.
A Patna based consulting firm was celebrating the success, so they organised a party for employees. In the party, total 3 types of cold drink were served, namely, Nimca, Disprite and Mountain Dew. It is known that total 400 members were present there but 22% members didn't drink any of the three types of cold drink. Further, it is known that total 600 bottles were served in the party.
The additional information is given below:
(1) The number of employees who drank both Nimca and Disprite was 5 more than the number of employees who drank both Disprite and Mountain Dew.
(2) The sum of the number of employees who drank Nimca and Disprite only and who drank Nimca and Mountain Dew only was equal to the number of employees who drank all the three types of cold drink
(3) The ratio of the total number of bottles of Mountain Dew to the total number of bottles of Disprite served was 37 : 43.
(4) The cold drinks were served in bottles only and no employee drank more than one bottle of the same type of cold drink.
(5) The number of employees who drank all the three types of cold drink was 80.
Q. What was the number of employees who drank both Disprite and Mountain Dew but not Nimca?
What is the angle between the lines represented by (x + y)2 - 3k(x + y) - 28k2 = 0?
Find the volume of a sphere whose radius is √2 times the radius of another sphere which exactly fits in a cube of side 18.
If log 2 = m, log 3 = a and log 7 = n, then the value of log (10!) in terms of m, a and n is
Which of the following numbers can never be a perfect square in any base system?
There are 24 points on a plane such that 10 of them are collinear. No 4 points are vertices of a cyclic quadrilateral. Find the maximum number of circles that can be drawn through any three points.
In a school of 600 students, 350 students are boys and the rest are girls. Ravi and Shweta were standing for the post of General Secretary. 60% of the boys voted for Ravi and the rest of the boys voted for Shweta. 60% of the girls voted for Shweta and the rest of the girls voted for Ravi. It was later found out that the voting machine was faulty and 50% of the boys who voted for Ravi had actually voted for Shweta and 60% of the boys who voted for Shweta had actually voted for Ravi. Also, 39% of the girls who voted for Ravi had actually voted for Shweta and 1/3rd of the girls who voted for Shweta had actually voted for Ravi. What is the absolute difference between the votes received by Ravi and Shweta?
(Assume that all the students voted)
How many distinct triangles have all three sides in integer units, none of which is a part of any Pythagorean Triplet?
The number of ways in which 16 sovereigns can be distributed among 3 applicants such that each applicant does not receive less than 3 sovereigns is:
The faces of a cube of n cm is first painted red and then the cube is cut into smaller cubes of 1cm. If the difference between the number of cubes with 1 face painted and the number with 2 faces painted is 90, what is the number of cubes with no face painted?
What is the remainder when 52 + 53 + 54 + ..... +5n,where n = 257, is divided by 52?