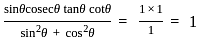RRB NTPC Mathematics Test - 2 (Hindi) - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test - RRB NTPC Mathematics Test - 2 (Hindi)
3 वर्षों के लिए 8,500 रूपये की जमा राशि पर साधारण ब्याज की राशि 2,040 रूपये है। तो वार्षिक ब्याज की दर ज्ञात कीजिये।
सुमित 3 वर्षों के लिए एक निश्चित ब्याज दर पर 29,700 रुपये पर साधारण ब्याज के रूप में 10,692 रुपये अर्जित करता है। उसका दोस्त अनिल समान ब्याज दर पर परन्तु वार्षिक चक्रवृद्धि ब्याज पर 2 वर्षों के लिए 12,500 रुपये का निवेश करता है। अनिल ब्याज के रूप में कितना अर्जित करता है?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
एक मिश्रण में दूध और पानी का अनुपात 9 ∶ 5 है। जब इस मिश्रण में 6 लीटर पानी मिलाया जाता है, तो दूध और पानी का अनुपात 9 ∶ 7 हो जाता है, मिश्रण में दूध की मात्रा ज्ञात कीजिए।
₹159250 की धनराशि को A, B, C और D के बीच इस प्रकार विभाजित किया जाता है कि A और B के हिस्से का अनुपात 1 : 3 है, B और C के हिस्से का अनुपात 2 : 5 है, तथा C और D के हिस्से का अनुपात 2 : 3 है। A का हिस्सा (₹ में) ज्ञात कीजिए।
मिश्र धातु A में धातुएँ x और y, 5 ∶ 2 के अनुपात में हैं, जबकि मिश्र धातु B में उनका अनुपात 3 ∶ 4 है। मिश्र धातु C मिश्र धातु A और B को 4 ∶ 5 के अनुपात में मिलाकर तैयार किया जाता है। मिश्र धातु C में x का प्रतिशत कितना है?
किसी धनराशि पर साधारण ब्याज, मूलधन का 2/25 गुना है, और वर्षों की संख्या, प्रति वर्ष दर प्रतिशत के 2 गुना के बराबर है। दर प्रतिशत ज्ञात कीजिए।
इंजन की खराबी के कारण, एक एक्सप्रेस ट्रेन अपनी सामान्य गति के 9/10 वीं गति से चलती है और 2: 28 बजे अपराह्न के बजाय 2: 34 बजे अपराह्न पर पहुंचती है। यह किस समय चलना शुरू हुई?
120 मीटर और 180 मीटर लंबाई की दो ट्रेनें विपरीत दिशाओं में 34 किमी/घंटा और 32 किमी/घंटा की समान गति से यात्रा कर रही हैं। दोनों ट्रेनों द्वारा एक दूसरे को पार करने में लिया गया समय कितना है?
एक समचतुर्भुज के एक विकर्ण की लम्बाई 30 सेमी है। यदि समचतुर्भुज का क्षेत्रफल 300 सेमी2 है, तो दूसरे विकर्ण की लम्बाई कितनी होगी?
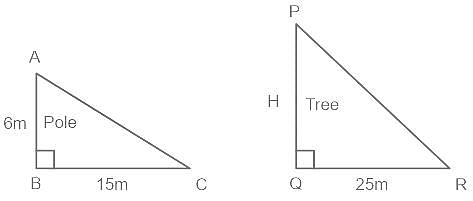
एक 6 मीटर ऊँचे खंभे की छाया 15 मीटर लम्बी है। यदि उसी समय एक पेड़ की छाया 25 मीटर लम्बी है, तो पेड़ की ऊँचाई कितनी होगी?
यदि secθ = 4/3 है, tan2 θ + tan4 θ का मान ज्ञात कीजिए।
एक निश्चित समय अवधि के बाद, बैंक में निवेश किए गए 24,000 रुपये की धनराशि 26,460 रुपये हो जाएगी, जब चक्रवृद्धि ब्याज दर 5% प्रति वर्ष है, जो वार्षिक संयोजित है। कितने महीनों में यह धनराशि 26,460 रुपये हो जाएगी?
निम्नलिखित दंड आलेख विभिन्न वर्षों में दुकानदारों A और B द्वारा बेचे गए कूलरों की संख्या को दर्शाता है। आलेख का अध्ययन करें और नीचे दिए गए प्रश्न का उत्तर दें।
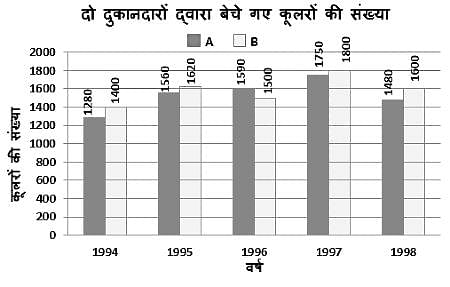
दुकानदार B द्वारा 1995 और 1998 में मिलाकर बेचे गए कूलरों की कुल संख्या, दुकानदार A द्वारा 1996 और 1997 में मिलाकर बेचे गए कूलरों की कुल संख्या से लगभग कितने प्रतिशत अधिक/कम है?
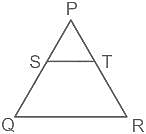
दी गई आकृति में ST || QR और ST ∶ QR = 3 ∶ 8 है। Δ PST और समलंब चतुर्भुज QRTS के क्षेत्रफलों का अनुपात है:
निम्न तालिका में, किसी कंपनी द्वारा अपनी स्थापना के बाद के वर्षों में निर्मित एलसीडी की बिक्री की संख्या दी गई है।
पिछले वर्षों में कम्पनी द्वारा बेचे गए एलसीडी के विभिन्न आकारों की संख्या (संख्या हजार में)
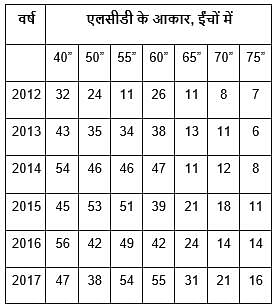
सभी छह वर्षों की कुल बिक्री किस आकार के "एलसीडी टीवी" के लिए न्यूनतम है?
यदि a + b = 20 और ab = 75 है, तो a3 + b3 का मान ज्ञात कीजिए।
एक परिवार का मासिक व्यय निम्नांकित वृत आलेख (पाई चार्ट) में दर्शाया गया है:
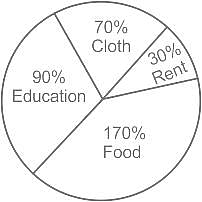
कुल मासिक व्यय में से शिक्षा पर व्यय का प्रतिशत कितना है?


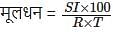
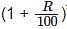 समय
समय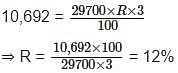
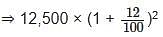

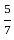
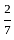
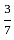
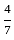
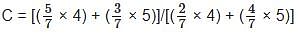
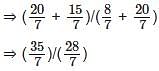

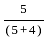
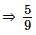
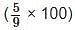
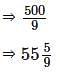
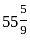 है।
है। 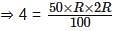
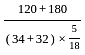 = 300 ×
= 300 × 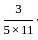 = 180/11
= 180/11 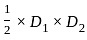 वर्ग इकाई है।
वर्ग इकाई है।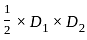
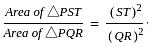
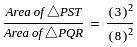
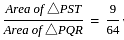
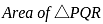 -
- 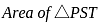
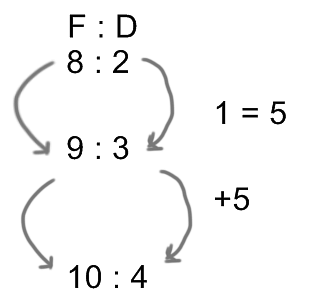
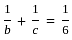


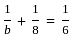

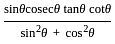 का मान क्या है?
का मान क्या है?