RRB NTPC Mathematics Test - 4 (Hindi) - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test - RRB NTPC Mathematics Test - 4 (Hindi)
निम्नलिखित विकल्पों में से कौन सा निकटतम अनुमानित मान है जो निम्नलिखित समीकरण में प्रश्न चिह्न (?) के स्थान पर आएगा?
104.96 + 120.96 + 103.16 - 12.89 × 2.04 + 124.93 ÷ 5.1 = ?
104.96 + 120.96 + 103.16 - 12.89 × 2.04 + 124.93 ÷ 5.1 = ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
दो बिंदु P और Q से एक मीनार के शीर्ष का उन्नयन कोण क्रमशः दूरी m2 और n2 पर है, जो आधार से और इसके साथ समान सीधी रेखा में एक-दूसरे के पूरक हैं। तो मीनार की ऊंचाई क्या है?
यदि a3 + 3a2 + 9a = 81 है, तो a3 + 3/a का मान क्या है?
दिशानिर्देश: निम्नलिखित वृत्त चित्र (पाई चार्ट) वर्ष 2020 में पाँच कंपनियों P, Q, R, S और T के व्यय (प्रतिशत में) को दर्शाता है?

Q, R और T कंपनी का कुल व्यय (करोड़ रुपये) में कितना था?
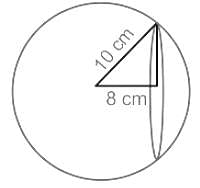
यदि 10 सेमी त्रिज्या के एक गोले को एक समतल द्वारा उसके केंद्र से 8 सेमी की दूरी पर प्रतिच्छेद किया जाता है, तो समतल और गोले के प्रतिच्छेदन वक्र की त्रिज्या कितनी है?
एक समबाहु त्रिभुज ABC का केन्द्रक G है और AB = 12 सेमी है। तो AG की लंबाई (सेमी में) है:
क्या प्रायिकता है कि दिसंबर के महीने में 5 रविवार हों?
सुरेश एक कार्य को 15 दिनों में कर सकता है। सुरेश और रमेश मिलकर उसी कार्य को 10 दिनों में करते हैं। यदि उन्हें कार्य के लिए 1500 रुपये का भुगतान किया जाता है, तो सुरेश और रमेश का हिस्सा (रुपये में) क्रमशः कितना होगा?
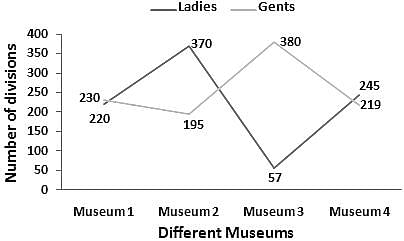
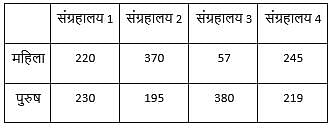
आरेख चार अलग-अलग संग्रहालयों- 1, 2, 3 और 4 में आगंतुकों की संख्या (महिला और पुरुष) को दर्शाता है। किस संग्रहालय में आगंतुकों की संख्या अधिकतम है?
यदि किसी वस्तु का अंकित मूल्य क्रय मूल्य से 25% अधिक है और वस्तु पर दी गई छूट 10% है। वस्तु पर लाभ प्रतिशत ज्ञात कीजिए
एक बस 2 घंटे के लिए औसतन 40 मील प्रति घंटे की गति से यात्रा करती है और फिर 3 घंटे के लिए 60 मील प्रति घंटे की गति से यात्रा करती है। बस ने पूरे 5 घंटे में कितनी दूरी तय की है?
मान ज्ञात कीजिए: 2 tan2 45° + cos2 30° - sin2 60°
निम्नलिखित में से कौन-सी संख्याएँ 2, 3 और 11 से विभाज्य हैं?
A. 8448
B. 9812
C. 9126
D. 9636
सही विकल्प का चयन कीजिए :
ΔABC में, ∠C = 90°, BC = AC = 3√2 है, तो AB = __________;


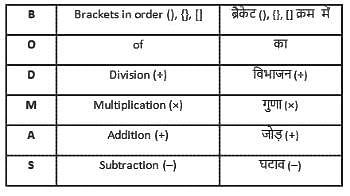

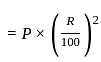 =
= 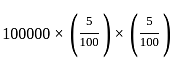 = रु 250
= रु 250














