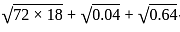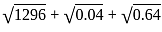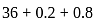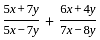RRB NTPC CBT 1 Question Paper (Held On: 29 Dec 2020 Shift 2) - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test - RRB NTPC CBT 1 Question Paper (Held On: 29 Dec 2020 Shift 2)
UNESCO का मुख्यालय कहाँ है?
तीन नल A, B और C एक टंकी को क्रमशः 15 घंटे, 12 घंटे और 18 घंटे में भर सकते हैं। यदि नल A और C दोनों को एकसाथ एक खाली टंकी में खोला जाता है, तब टंकी को भरने में लिया गया समय (घंटे में) होगा:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
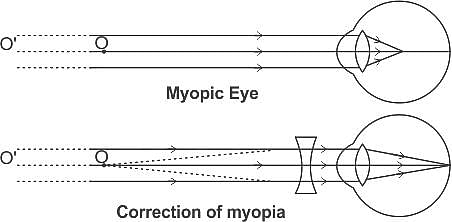
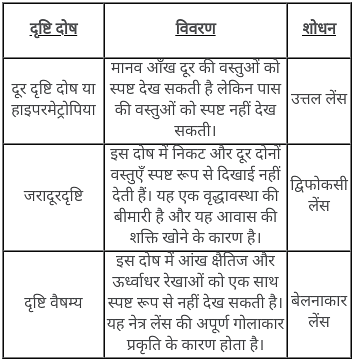
निकट दृष्टि दोष वाले व्यक्ति की दृष्टि को ठीक करने के लिए किस प्रकार के लेंस की आवश्यकता होती है?
जिम कॉर्बेट राष्ट्रीय उद्यान _______ में स्थित है
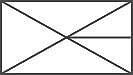
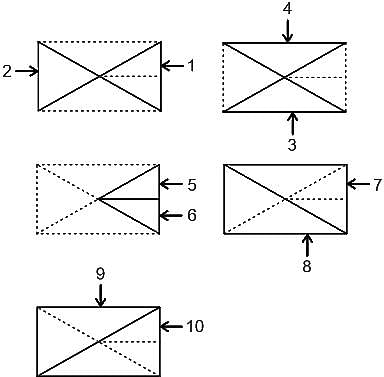
निम्नलिखित आकृति में कितने त्रिभुज हैं?
GST भारत में लगाया जाने वाला एक अप्रत्यक्ष कर है। GST का पूर्ण रूप क्या है?
एक संख्या में 22(1/2)% की कमी करने पर वह 217 हो जाती है। वह संख्या ज्ञात कीजिए।
भारतीय केंद्रीय औषधि अनुसंधान संस्थान कहाँ स्थित है?
हुमायूँ-नामा _____ द्वारा लिखा गया था
जातक कथाएँ _____ से संबंधित हैं।
इसरो ने फरवरी, 2017 में ______ प्रक्षेपण करके इतिहास रच दिया।
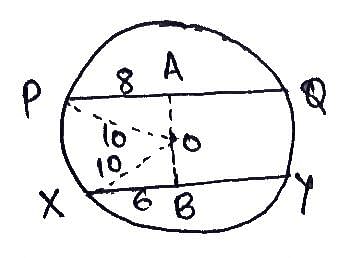
एक वृत्त में जिसकी त्रिज्या 10 सेमी है, XY और PQ दो समानांतर जीवाएँ हैं जिनकी लंबाई क्रमशः 12 सेमी और 16 सेमी है। दो जीवाएँ केंद्र के विपरीत दिशा में स्थित हैं। जीवाओं के बीच की दूरी क्या है?
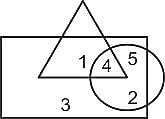
अनेक आकृतियों वाली दी गई आकृति में, कौन-सी संख्या केवल एक ही आकृति में मौजूद है?
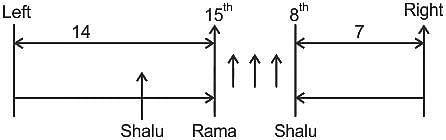
लड़कियों की एक पंक्ति उत्तर की ओर उन्मुख खड़ी है। रमा बाएँ से पंद्रहवें स्थान पर हैं और शालू दाएँ से आठवें स्थान पर है। यदि शालू को बाईं ओर पाँच स्थानों से स्थानांतरित किया जाता है, तब वह रमा के ठीक बाईं ओर चली जाती है। पंक्ति में कितनी लड़कियाँ खड़ी हैं?
दिए गए कथनों और निष्कर्षों को ध्यानपूर्वक पढ़िए। यह मानते हुए कि कथनों में दी गई जानकारी सत्य है, भले ही वह सामान्य रूप से ज्ञात तथ्यों से भिन्न प्रतीत होती हो, तय कीजिए कि दिए गए निष्कर्षों में से कौन-सा/से निष्कर्ष कथनों का तार्किक रूप से अनुसरण करता/करते है/हैं।
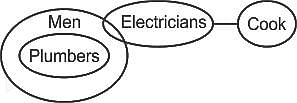
कथन:
1. सभी प्लंबर पुरुष हैं।
2. कुछ पुरुष इलेक्ट्रीशियन हैं।
3. कोई इलेक्ट्रीशियन रसोइया नहीं है।
निष्कर्ष:
1. कुछ प्लंबर रसोइया हैं।
2. कुछ प्लंबर रसोइया नहीं हैं।
3. कुछ पुरुष रसोइया नहीं हैं।
यदि x/y = 4/5 है, तब 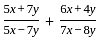 का मान किसके बराबर है?
का मान किसके बराबर है?
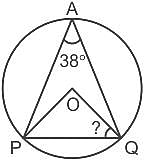
दी गयी आकृति में, PO और OQ, ∆APQ के परिवृत्त की त्रिज्याएँ हैं। यदि ∠PAQ = 38°, है तब ∠PQO का मान क्या होगा?
यदि 3 cosθ = √3 है, तब cosec θ . tan θ का मान क्या है?
निम्नलिखित में से कौन सा स्थान यूरेनियम के खनन के लिए प्रसिद्ध है?
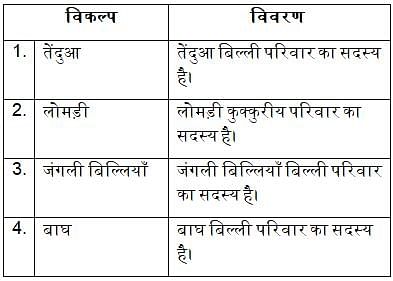
चार शब्द दिए गए हैं, जिनमें से तीन किसी प्रकार से आपस में संबंधित हैं जबकि, एक भिन्न है। जो भिन्न है, उसका चयन कीजिए।


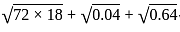 का मान है:
का मान है: