Mathematics Test - 1 - SAT MCQ
30 Questions MCQ Test - Mathematics Test - 1
The nth term of a sequence is given by the expression bn + 4, where b is a positive constant. Which of the following is necessarily equal to b ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
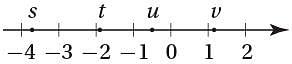
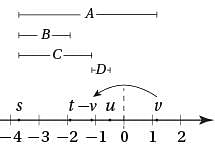
If s, t, u, and v are the coordinates of the indicated points on the number line above, which of the following is greatest?
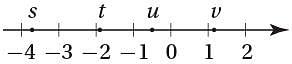
If s, t, u, and v are the coordinates of the indicated points on the number line above, which of the following is greatest?
The Municipal Electric Company charges each household $0.15 per kilowatt-hour of electricity plus a flat monthly service fee of $16. If a household uses 30 kilowatt-hours of electricity and is charged $P in a given month, which of the following equations is true?
If a and b are the coordinates of two points on the number line, then which of the following is equivalent to the statement that the absolute distance from a to b is greater than the absolute distance from -2 to 6 ?
In a survey of 80 students, 55 students stated that they play a varsity sport, and 35 stated that they are taking at least one AP level course. Which of the following statements must be true?
Let function f(x) be defined by the equation f (x) = x2 - 1. If b is a positive real number, then f(1/b) =
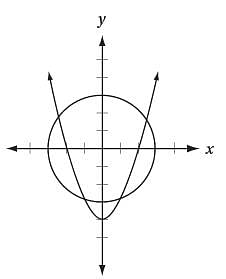
x2 + y2 = 9
y = x2 - 4
A system of two equations and their graphs in the xy-plane are shown above. How many solutions does the system have?
What is the total number of x- and y-intercepts in the graph of the equation y = (x + 2)2(x - 3)2?
The average (arithmetic mean) of three numbers is 50. If two of the numbers have a sum of 85, what is the third number?
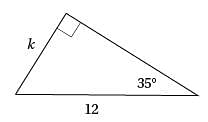
In the triangle above, what is the value of k? (sin 35° = 0.574, cos 35° = 0.819, tan 35° = 0.700)
y = -3(x - 2)2 + 2
In the xy-plane, line l passes through the point (-1, 3) and the vertex of the parabola with equation above. What is the slope of line l?
Which of the following is equal to a2/3, for all values of a ?
The equation 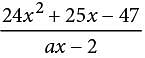 = -8x - 3
= -8x - 3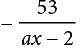 for all values of x ≠ 2/α, where α is a constant.What is the value of α?
for all values of x ≠ 2/α, where α is a constant.What is the value of α?
Two isosceles triangles are shown above. If 180 − z = 2y and y = 75, what is the value of x ?
The average number of students per classroom at Central High School from 2000 to 2010 can be modeled by the equation y = 0.56x + 27.2, where x represents the number of years since 2000, and y represents the average number of students per classroom. Which of the following best describes the meaning of the number 0.56 in the equation?
Question refer to the following information.
S(P) = 1/2 P + 40
D(P) = 220 - P
The quantity of a product supplied and the quantity of the product demanded in an economic market are functions of the price of the product. The functions above are the estimated supply and demand functions for a certain product. The function S(P) gives the quantity of the product supplied to the market when the price is P dollars, and the function D(P) gives the quantity of the product demanded by the market when the price is P dollars.
Q. At what price will the quantity of the product supplied to the market equal the quantity of the product demanded by the market?
Which of the following is an example of a function whose graph in the xy-plane has no x-intercepts?
y = x2
2y + 6 = 2(x + 3)
If (x, y) is a solution of the system of equations above and x > 0, what is the value of xy?
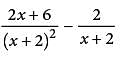
The expression above is equivalent to 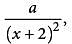 where a is a positive constant and x ≠ − 2. What is the value of a?
where a is a positive constant and x ≠ − 2. What is the value of a?
In the 1908 Olympic Games, the Olympic marathon was lengthened from 40 kilometers to approximately 42 kilometers. Of the following, which is closest to the increase in the distance of the Olympic marathon, in miles? (1 mile is approximately 1.6 kilometers.)
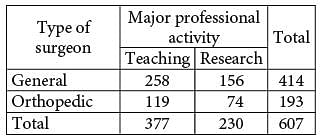
In a survey, 607 general surgeons and orthopedic surgeons indicated their major professional activity.
The results are summarized in the table above. If one of the surgeons is selected at random, which of the following is closest to the probability that the selected surgeon is an orthopedic surgeon whose indicated professional activity is research?
αx3 + bx2 + cx + d = 0
In the equation above, α, b, c, and d are constants.
If the equation has roots −1 , −3 , and 5, which of the following is a factor of αx3 + bx2 + cx + d?
The expression 1/3 x2 - 2 can be rewritten as 1/3 (x - k) (x + k), where k is a positive constant.What is the value of k ?
(7532 + 100y2) + 10(10y2 − 110)
The expression above can be written in the form αy2 + b , where α and b are constants. What is the value of α + b ?
If 50 one-cent coins were stacked on top of each other in a column, the column would be approximately 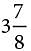 inches tall. At this rate, which of the following is closest to the number of one-cent coins it would take to make an 8-inch-tall column?
inches tall. At this rate, which of the following is closest to the number of one-cent coins it would take to make an 8-inch-tall column?


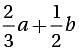 = 5, and b = 4, what is the value of α?
= 5, and b = 4, what is the value of α?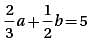
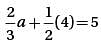
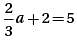
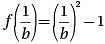
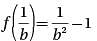
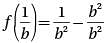
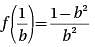
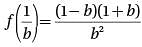
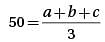
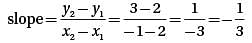
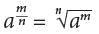 for any positive integers m and n. It follows, therefore, that
for any positive integers m and n. It follows, therefore, that 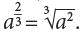
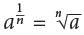 for any positive integer n.
for any positive integer n.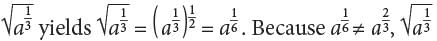 is not the correct answer. Choice B is incorrect. By definition,
is not the correct answer. Choice B is incorrect. By definition, 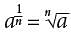 for any positive integer n.
for any positive integer n.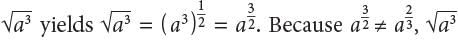 is not the correct answer. Choice C is incorrect. By definition,
is not the correct answer. Choice C is incorrect. By definition, 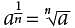 for any positive integer n. Applying this definition as well as the power property of exponents to the expression
for any positive integer n. Applying this definition as well as the power property of exponents to the expression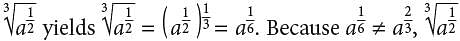 is not the correct answer.
is not the correct answer.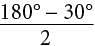 = 75°. Therefore, the measure of the angle marked x° is 180° − 75° = 105°, and so the value of x is 105.
= 75°. Therefore, the measure of the angle marked x° is 180° − 75° = 105°, and so the value of x is 105.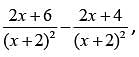 which is equivalent to
which is equivalent to 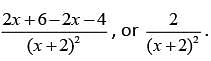 This is in the form
This is in the form 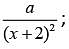 therefore, a = 2.
therefore, a = 2.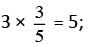 however, 9/5 is not equal to 5.
however, 9/5 is not equal to 5. 
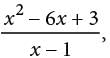 what is f(−1) ?
what is f(−1) ?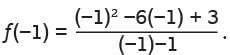 Simplifying the expressions in the numerator and denominator yields
Simplifying the expressions in the numerator and denominator yields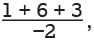 which is equal to 10/-2 or –5.
which is equal to 10/-2 or –5.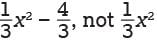 − 2. Choice B is incorrect. This may result from incorrectly factoring the expression and finding (x – 6) (x + 6) as the factored form of the expression. Choice C is incorrect. This may result from incorrectly distributing the 1/3 and rewriting the expression as 1/3 (x2 − 2).
− 2. Choice B is incorrect. This may result from incorrectly factoring the expression and finding (x – 6) (x + 6) as the factored form of the expression. Choice C is incorrect. This may result from incorrectly distributing the 1/3 and rewriting the expression as 1/3 (x2 − 2).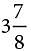 inches tall, which is slightly less than 4 inches tall. Therefore a column of stacked one-cent coins that is 4 inches tall would contain slightly more than 50 one-cent coins. It can then be reasoned that because 8 inches is twice 4 inches, a column of stacked one-cent coins that is 8 inches tall would contain slightly more than twice as many coins; that is, slightly more than 100 one-cent coins. An alternate approach is to set up a proportion comparing the column height to the number of one-cent coins, or
inches tall, which is slightly less than 4 inches tall. Therefore a column of stacked one-cent coins that is 4 inches tall would contain slightly more than 50 one-cent coins. It can then be reasoned that because 8 inches is twice 4 inches, a column of stacked one-cent coins that is 8 inches tall would contain slightly more than twice as many coins; that is, slightly more than 100 one-cent coins. An alternate approach is to set up a proportion comparing the column height to the number of one-cent coins, or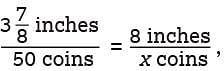 where x is the number of coins in an 8-inch-tall column. Multiplying each side of the proportion by 50x gives
where x is the number of coins in an 8-inch-tall column. Multiplying each side of the proportion by 50x gives 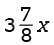 = 400. Solving for x gives x =
= 400. Solving for x gives x = 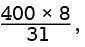 which is approximately 103. Therefore, of the given choices, 100 is closest to the number of one-cent coins it would take to build an 8-inch-tall column.
which is approximately 103. Therefore, of the given choices, 100 is closest to the number of one-cent coins it would take to build an 8-inch-tall column.














