Mathematics Test - 5 - SAT MCQ
30 Questions MCQ Test - Mathematics Test - 5
If f (x) = 3x + n, where n is a constant, and f (2) = 0, then f(n) =
x - 3y = -2
y= 5/x
The values of x that satisfy the system of equations above also satisfy which of the following equations?
y= 5/x
The values of x that satisfy the system of equations above also satisfy which of the following equations?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The bird department of a pet store has 12 canaries, 30 finches, and 18 parrots. If the pet store purchased n more finches, then 80% of its birds would be finches. Which of the following equations must be true?
The cost in dollars, C, to manufacture n necklaces is given by the equation C(n) = an + b, where a and b are positive constants. In this equation, what does a represent?
The graph of the equation y = 2x2 - 16x + 14 intersects the y-axis at point A and the x-axis at points B and C. What is the area of triangle ABC?
a - b = 10
a - 2b = 8
Based on the system of equations above, what is the value of b?
Which of the following statements expresses the fact that the product of two numbers, a and b, is 6 greater than their sum?
A jar contains only red, white, and blue marbles. It contains twice as many red marbles as white marbles and three times as many white marbles as blue marbles. If a marble is chosen at random, what is the probability that it is not red?
Let function f(x) be defined by the equation 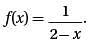 If m is a positive integer, then f(1/m) =
If m is a positive integer, then f(1/m) =

The function f is defined by a polynomial. Some values of x and f(x) are shown in the table above. Which of the following must be a factor of f(x) ?
y = α(x − 2)(x + 4)
In the quadratic equation above, a is a nonzero constant. The graph of the equation in the xy-plane is a parabola with vertex (c, d). Which of the following is equal to d?
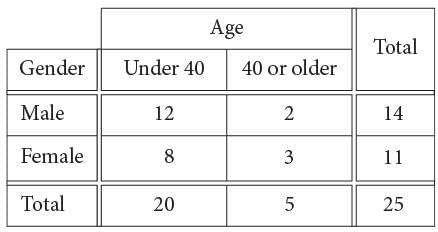
The table above shows the distribution of age and gender for 25 people who entered a contest. If the contest winner will be selected at random, what is the probability that the winner will be either a female under age 40 or a male age 40 or older?
Question refer to the following information.
S(P) = 1/2 P + 40
D(P) = 220 - P
The quantity of a product supplied and the quantity of the product demanded in an economic market are functions of the price of the product. The functions above are the estimated supply and demand functions for a certain product. The function S(P) gives the quantity of the product supplied to the market when the price is P dollars, and the function D(P) gives the quantity of the product demanded by the market when the price is P dollars.
Q. How will the quantity of the product supplied to the market change if the price of the product is increased by $10 ?
The sum of three numbers is 855. One of the numbers, x, is 50% more than the sum of the other two numbers. What is the value of x ?
In air, the speed of sound S, in meters per second, is a linear function of the air temperature T, in degrees Celsius, and is given by S(T) = 0.6T + 331.4.
Which of the following statements is the best interpretation of the number 331.4 in this context?
At a restaurant, n cups of tea are made by adding t tea bags to hot water. If t = n + 2, how many additional tea bags are needed to make each additional cup of tea?
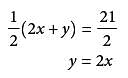
The system of equations above has solution (x,y). What is the value of x?
Which of the following is an equivalent form of (1.5x − 2.4)2 − (5.2x2 − 6.4)?
y < 3x +1
x - y >1
Which of the following ordered pairs (x, y) satisfies the system of inequalities above?
Question refer to the following information.

One method of calculating the approximate age, in years, of a tree of a particular species is to multiply the diameter of the tree, in inches, by a constant called the growth factor for that species. The table above gives the growth factors for eight species of trees.
If a white birch tree and a pin oak tree each now have a diameter of 1 foot, which of the following will be closest to the difference, in inches, of their diameters 10 years from now? (1 foot = 12 inches)
Question refer to the following information.
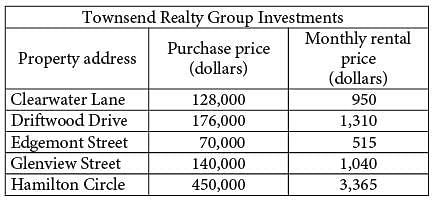
The Townsend Realty Group invested in the five different properties listed in the table above. The table shows the amount, in dollars, the company paid for each property and the corresponding monthly rental price, in dollars, the company charges for the property at each of the five locations.
The relationship between the monthly rental price r, in dollars, and the property’s purchase price p, in thousands of dollars, can be represented by a linear function. Which of the following functions represents the relationship?
The graph of a line in the xy-plane passes through the point (1, 4) and crosses the x-axis at the point (2, 0). The line crosses the y-axis at the point (0, b).
What is the value of b ?
A market researcher selected 200 people at random from a group of people who indicated that they liked a certain book. The 200 people were shown a movie based on the book and then asked whether they liked or disliked the movie. Of those surveyed, 95% said they disliked the movie. Which of the following inferences can appropriately be drawn from this survey result?
9αx + 9b − 6 = 21
Based on the equation above, what is the value of αx + b ?
Question refer to the following information.
Mosteller’s formula: A = 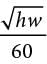
Current’s formula: A = 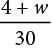
The formulas above are used in medicine to estimate the body surface area A, in square meters, of infants and children whose weight w ranges between 3 and 30 kilograms and whose height h is measured in centimeters.
Q. Based on Current’s formula, what is w in terms of A ?


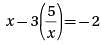
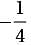
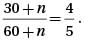
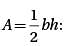
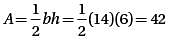
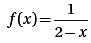
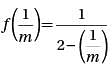
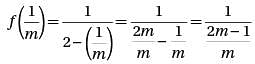
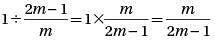
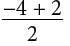 = −1. This is the value of c. To find the y-coordinate of the vertex, substitute −1 for x in y = α(x − 2)(x + 4): y = α(x − 2)(x + 4) = α(−1 − 2)(−1 + 4) = α(−3)(3) = −9α.
= −1. This is the value of c. To find the y-coordinate of the vertex, substitute −1 for x in y = α(x − 2)(x + 4): y = α(x − 2)(x + 4) = α(−1 − 2)(−1 + 4) = α(−3)(3) = −9α.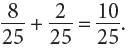
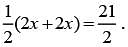 Dividing both sides of this equation by 1/2 yields (2x + 2x )= 21 . Combining like terms results in 4x = 21. Finally, dividing both sides by 4 gives x = 21/4 = 5.25. Either 21/4 or 5.25 can be gridded as the correct answer.
Dividing both sides of this equation by 1/2 yields (2x + 2x )= 21 . Combining like terms results in 4x = 21. Finally, dividing both sides by 4 gives x = 21/4 = 5.25. Either 21/4 or 5.25 can be gridded as the correct answer.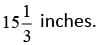 The difference between
The difference between 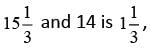 or approximately 1.3 inches.
or approximately 1.3 inches.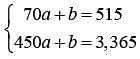
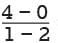 = −4. So, the equation of the line is of the form y = −4x + b. Since (2, 0) satisfies this equation, 0 = −4(2) + b must be true. Solving this equation for b gives b = 8.
= −4. So, the equation of the line is of the form y = −4x + b. Since (2, 0) satisfies this equation, 0 = −4(2) + b must be true. Solving this equation for b gives b = 8.
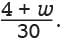 Multiplying each side of the equation by 30 gives 30A = 4 + w. Subtracting 4 from each side of 30A = 4 + w gives w = 30A – 4.
Multiplying each side of the equation by 30 gives 30A = 4 + w. Subtracting 4 from each side of 30A = 4 + w gives w = 30A – 4.














