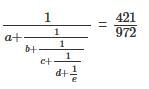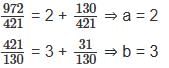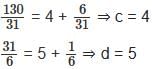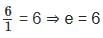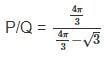Test: Elementary Mathematics - 3 - CDS MCQ
30 Questions MCQ Test - Test: Elementary Mathematics - 3
If p is the perimeter of the smallest sector, then what is the value of 9p?
If t = cos 79°, then what is cosec 79° (1 - cos 79°) equal to ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
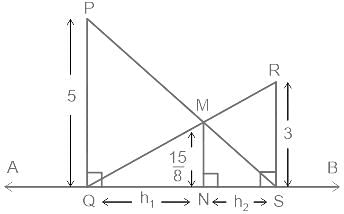
What is the ratio of the area of the quadrilateral PQNM to the area of the quadrilateral RSNM?
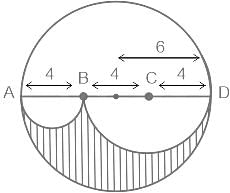
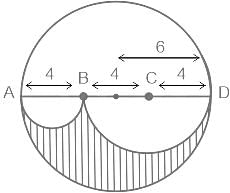
What is the area of the non - overlapping region?
What is the area of the region between two concentric circles, if the length of a chord of the outer circle touching the inner circle at a particular point of its circumference is 14 cm ? (Takе π = 22/7)
In a right - angled triangle ABC, AB = 15 cm, BC 20 cm and AC = 25 cm. Further, BP is the perpendicular on AC. What is the difference in the area of triangles PAB and PCB ?
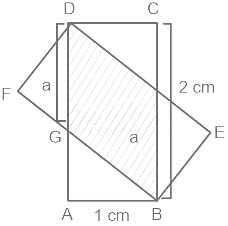
In a quadrilateral ABCD, AB = 6 cm, BC = 18 cm, CD = 6 cm and DA = 10 cm. If the diagonal BD = x, then which one of the following is correct?
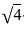 ∶
∶ 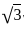 ∶
∶ 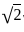 ∶
∶  , then what is the value of
, then what is the value of 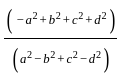 ?
?
If the people coming from a particular State belonging to S are 15% and 24,000 in number, then what is the total number of migrating people belonging to the age group B ?
A cube whose edge is 14 cm long has on each of its faces a circle of 7 cm radius painted yellow. What is the total area of unpainted surface? (Takе π = 22/7)
What is the ratio of the area of the shaded region to that of the non - shaded region?
Consider the following for the next ten (10) items that follow:
Each item contains a Question followed by two Statements. Answer each item using the following instructions:
Question : Is xy positive?
Statement - I : x = 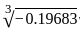
Statement - II : y = 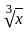
What is the maximum of differences between the number of people coming from different groups P, Q, R and S? (We can use the data given in the previous questions)
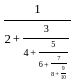 , then which one of the following is correct?
, then which one of the following is correct?
Consider the following for the next ten (10) items that follow:
Each item contains a Question followed by two Statements. Answer each item using the following instructions:
Area of a rectangle with length x and breadth y is P and area of a parallelogram (which is strictly not a rectangle) with adjacent sides of length x and y is Q.
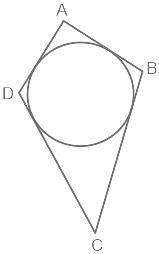
A circle touches all the four sides AB, BC, CD, DA of a quadrilateral ABCD.
Question : What is the perimeter of the quadrilateral ?
Statement - I : AB + DC = 10 cm
Statement - II : AD + BC = 10 cm
If 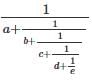 =
= 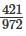 , then what is the value of a × b × c × d × e?
, then what is the value of a × b × c × d × e?
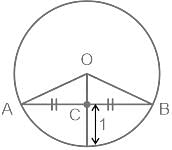
The chord AB of a circle with centre at O is 2√3 times the height of the minor segment. If P is the area of the sector OAB and Q is the area of the minor segment of the circle, then what is the approximate value of P/Q ?
(Take √3 = 1.7 and π = 3.14)


 (1 - t)
(1 - t)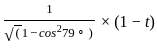
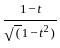
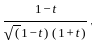

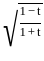 .
.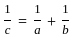
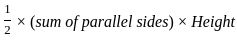

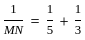
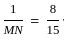
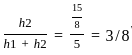
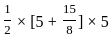
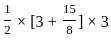
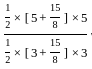 = 275/117
= 275/117 +
+ 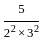 +
+  + ... equal to ?
+ ... equal to ?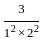 +
+  +
+ 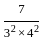 + ...
+ ... 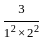 +
+ 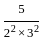 +
+  + ...
+ ... 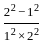 +
+ 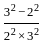 +
+  + ...
+ ... 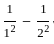 +
+  +
+ 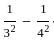 + ...... -
+ ...... - 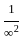
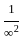


 ∶
∶ 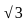 ∶
∶ 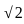 ∶
∶ 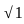
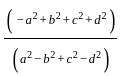

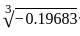
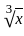
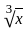

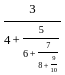
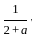
 will always be less then
will always be less then 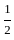 = 0.5
= 0.5