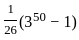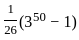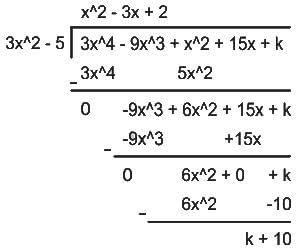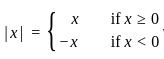Test: Elementary Mathematics - 8 - CDS MCQ
30 Questions MCQ Test - Test: Elementary Mathematics - 8
If the mean of 10, 4, 5, 3, 2, 6, 7, 3 is m and the mean of 2, 5, 3, 11, m, 10 is p, then what is the value of (m + p) ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If sin α + cos α = 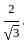 , then what is (tan α + cot α) equal to?
, then what is (tan α + cot α) equal to?
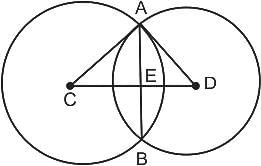
Two circles with diameters 50 cm and 58 cm, respectively, intersect each other at points A and B, such that the length of the common chord is 40 cm. Find the distance (in cm) between the centres of these two circles.
If two zeroes of the polynomial x3 + 7x2 - 2x - 14 are √2 and -√2, then the third zero is
A batsman scored 135 runs in his 12th match. The average run scored by the batsman in 11 matches is x. If the average run scored by a batsman is increased by 5 runs, then find the new average after his 12th match.
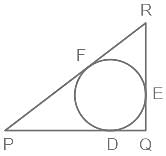
In the given figure, a circle is inscribed in ΔPQR, such that it touches the sides PQ, QR and RP at points D, E, F, respectively. If the lengths of the sides PQ = 18 cm. QR = 13 cm and RP = 15 cm, then find the length of PD.
What is the area of the equilateral triangle, if the perimeter of the equilateral triangle is equal to the circumference of the circle whose radius is (OA + 16) cm?
The age of 4 persons are in the ratio of 13 ∶ 21 ∶ 10 ∶ 25, and their average age is 69 years. Find the difference between the age of the oldest and the youngest person.
Add the following term 9a3 + 8b3 - c3 + a3 - 4b3 + 3 and find out the co-efficient of c3.
a) -1
b) 1
c) 10
d) 3
Two persons Ram and Shyam can dig a pit in 25 days and 30 days respectively and a third person Mohan can fill that pit in 75 days. All of the three persons start their work and after some time Mohan leaves the work. If the total time taken to dig the pit from the beginning is 15 days, find after how many days Mohan left his work.
The average weight of a class of 15 students is 42. If the teacher is included, the average weight increases by 1 kg. What is the weight of the teacher?
For what value of k, is the polynomial f(x) = 3x4 - 9x3 + x2 + 15x + k completely divisible by 3x2 - 5?
At 7 : 30 P.M. the owner of a Cycle noticed that a thief is taking away his cycle from his home and is cycling in a particular direction at an estimated speed of 10 km per hour. He informed the police about the theft and the policeman started from the same point, half an hour later than the time of the theft but with a speed of 12 km per hour. At what time will Policeman catch the thief?
A bottle with the cost price of Rs. 4500 is marked x% above the cost price and sold after two successive discount of Rs. 140 and 10% respectively for a profit of Rs. 720. A jeans has cost price that is 20% less than that of the bottle. If the selling price of the jeans is Rs.4680 and it is sold at (x - k)% profit then find the value of k?
If the length of MC is k cm, the length of BC is
α and β are distinct real roots of the quadratic equation x2 + ax + b = 0. Which of the following statements is/are sufficient to find α ?
1. α + β = 0, α2 + β2 = 2
2. αβ2 = -1, a = 0
Select the correct answer using the code given below :


 ,
,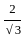

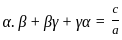
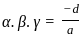


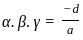
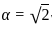 and
and 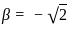
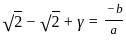
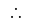 Option 2 is correct.
Option 2 is correct.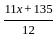 = x + 5
= x + 5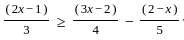 is
is