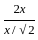Test: Elementary Mathematics - 9 - CDS MCQ
30 Questions MCQ Test - Test: Elementary Mathematics - 9
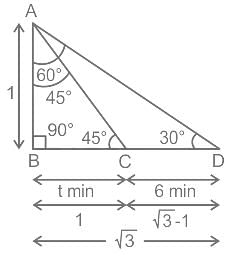
A person on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes 6 minutes for the angle of depression to change from 30° to 45°, and further t minutes to reach the tower, which one of the following is correct ?
The time taken by a train to cross a man travelling in another train is 10 seconds, when the other train is travelling in the opposite direction. However, it takes 20 seconds, if both the trains are travelling in the same direction. The length of the first train is 200 m and that of the second train is 150 m. What is the speed of the first train ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let x be the area of a square inscribed in a circle of radius r and y be the area of an equilateral triangle inscribed in the same circle. Which one of the following is correct ?
What is the largest number which divides both 235 - 1 and 291 - 1 ?
Item contains a Question followed by two Statements. Answer each item using the following instructions :
Question: Is triangle right angled ?
Statement I: The length of the line segment joining the mid-points of two sides of a triangle is half of the third side of the triangle.
Statement II: The angles of a triangle are in the ratio 1 : 2 : 3
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. What is the area of the sector ?
What is the value of (1 + cot2 θ) (1 + cos θ) (1 - cos θ) - (1 + tan2 θ) (1 + sin θ) (1 - sin θ) ?
If 2 cos2 θ + sin θ - 2 = 0, 0 < θ ≤ π/2, then what is the value of θ ?
Item contains a Question followed by two Statements. Answer each item using the following instructions :
Question: Can a circle be drawn through the points A, B and C ?
Statement I: AB = 5 cm, BC = 5 cm, CA = 6 cm.
Statement II: AB = 3 cm, BC = 4 cm, CA = 7 cm.
Item contains a Question followed by two Statements. Answer each item using the following instructions :
Question: Is m > n, where m, n are non-zero numbers ?
Statement I: 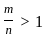
Statement II: m > 2n
A woman is standing on the deck of a ship, which is h (in metres) above water level. She observes the angle of elevation of the top of a tower as 60° and the angle of depression of the base of the tower as 30°. What is the height of the tower ?
Consider the following statements in respect of all factors of 360 :
1. The number of factors is 24.
2. The sum of all factors is 1170.
Which of the above statements is/are correct ?
The surface area of a cube is increased by 25%. If p is the percentage increase in its length, then which one of the following is correct ?
If the length of a rectangle is increased by 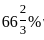 , then by what percent should the width of the rectangle be decreased in order to maintain the same area ?
, then by what percent should the width of the rectangle be decreased in order to maintain the same area ?
If tan8 θ + cot8 θ = m, then what is the value of tan θ + cot θ ?
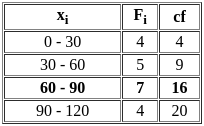
If the median (P) and mode (Q) satisfy the relation 7(Q - P) = 9R, then what is the value of R?
In a party of 150 persons, 75 persons take tea, 60 persons take coffee and 50 persons take milk. 15 of them take both tea and coffee, but no one taking milk takes tea. If each person in the party takes at least one drink, then what is the number of persons taking milk only ?
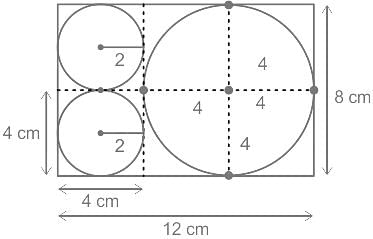
What is the maximum area that can be covered by three non-intersecting circles drawn inside a rectangle of sides 8 cm and 12 cm?
Item contains a Question followed by two Statements. Answer each item using the following instructions :
Question: What are the unique values of a, b and c if 2 is a root of the equation ax2 + bx + c = 0 ?
Statement I: Ratio of c to a is 1.
Statement II: Ratio of b to a is (-5/2).
Item contains a Question followed by two Statements. Answer each item using the following instructions :
Question: Can the value of (x + y) be determined uniquely?
Statement I: (x + y)4 = 256.
Statement II: (x + y)3 < 16.
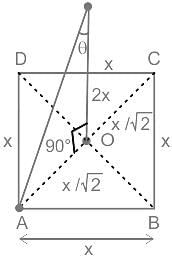
ABCD is a square field with AB = x. A vertical pole OP of height 2x stands at the centre O of the square field. If ∠APO = θ, then what is cot θ equal to ?
A solid iron ball is melted and 64 smaller solid balls of equal size are made using the entire volume of iron. What is the ratio of the surface area of the larger ball to the sum of the surface areas of all the smaller balls ?
Consider the following statements :
1. n3 - n is divisible by 6.
2. n5 - n is divisible by 5.
3. n5 - 5n3 + 4n is divisible by 120.
Which of the statements given above are correct ?
If α and β are the roots of the equation x2 - 7x + 1 = 0, then what is the value of α4 + β4 ?


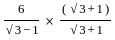
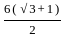 [∵ (a2 - b2) = (a - b)(a + b)]
[∵ (a2 - b2) = (a - b)(a + b)]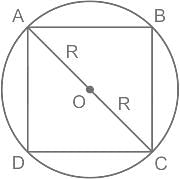

 r2 -
r2 - 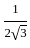 r2 =
r2 = 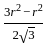


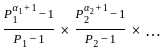
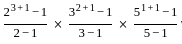
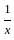 )2 = (x2 +
)2 = (x2 + 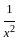 ) + 2
) + 2


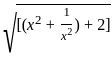
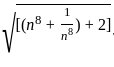
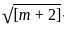
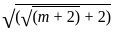
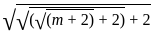
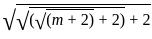

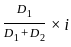
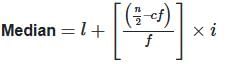
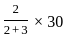 = 72
= 72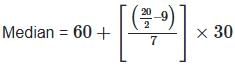

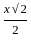 =
= 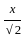
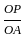 =
=