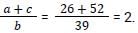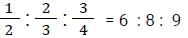Test: SSC CGL Previous Year Question: Number System and HCF & LCM (2023-2024) - 1 - SSC CGL MCQ
30 Questions MCQ Test - Test: SSC CGL Previous Year Question: Number System and HCF & LCM (2023-2024) - 1
If the 5-digit number 676xy is divisible by 3, 7 and 11, then what is the value of (3x - 5y)? [SSC CGL 13/08/2021 (Morning)]
Find the difference between squares of the greatest value and the smallest value of P if the number 5306P2 is divisible by 3. [SSC CGL 16/08/2021 (Evening)]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the seven-digit number 94x29y6 is divisible by 72, then what is the value of (2x + 3y) for x ≠ y? [SSC CGL 17/08/2021 (Morning)]
If a number P is divisible by 2 and another number Q is divisible by 3, then which of the following is true? [SSC CGL 18/08/2021 (Evening)]
The average of squares of five consecutive odd natural numbers is 233. What is the average of the largest number and the smallest number? [SSC CGL 20/08/2021 (Morning)]
If the 5-digit number 593ab is divisible by 3, 7 and 11, then what is the value of (a2 - b2 + ab)? [SSC CGL 23/08/2021 (Morning)]
If the six-digit number 5z3x4y is divisible by 7, 11 and 13, then what is the value of (x + y - z)? [SSC CGL 23/08/2021 (Afternoon)]
Find the sum of all the possible values of (a + b), so that number 4a067b is divisible by 11. [SSC CGL 24/08/2021 (Afternoon)]
Two positive numbers differ by 1280. When the greater number is divided by the smaller number, the quotient is 7 and the remainder is 50. The greater number is: [SSC CGL Tier II (15/11/2020)]
When positive numbers x, y and z are divided by 31, the reminders are 17, 24 and 27 respectively. When (4x - 2y + 3z) is divided by 31, the reminder will be : [SSC CGL Tier II (15/11/2020)]
If the five digit number 235xy is divisible by 3, 7 and 11 then what is the value of (3x - 4y)? [SSC CGL Tier II (16/11/2020)]
When 7897, 8110 and 8536 are divided by the greatest number x, then the remainder in each case is the same. The sum of the digits of x is : [SSC CGL Tier II (11/09/2019)]
Let a, b and c be the fractions such that a ≺ b ≺ c. If c is divided by a, the result is 5/2, which exceeds b by 7/4. If a + b + c = 1(11/12), then (c - a) will be equal to : [SSC CGL Tier II (11/09/2019)]
Three fractions, x, y and z, are such that x > y > z. When the smallest of them is divided by the greatest, the result is 9/16, which exceeds y by 0.0625. If x + y + z = 1(13/24), then the value of x + z is : [SSC CGL Tier II (12/09/2019)]
What is the least value of X such that 517X 324 is divisible by 12? [SSC CGL 11/06/2019 (Morning)]
13, a, b, c are four distinct numbers and the HCF of each pair of numbers (13, a) : (13, b) : (13, c) is 13, where a, b, c are each less than 60 and a < b < c. What is the value of ((a + c)/b)? [SSC CGL 13/04/2021 (Morning)]
Find the least number divisible by 2, 3, 5, 6, 9 and 18, which is a perfect square. [SSC CGL 24/07/2023 (2nd shift)]
The product of the two numbers is 1500 and their HCF is 10. The number of such possible pairs is/are: [SSC CGL Tier II (02/03/2023)]
If the highest common factor (HCF) of x and y is 15, then the HCF of 36x2 - 81y2 and 81x2 - 9y2 is divisible by [SSC CGL Tier II (06/03/2023)]
What will be the least number which when doubled will be exactly divisible by 15, 18, 25 and 32? [SSC CGL 02/12/2022 (2nd Shift)]
Calculate the HCF of 12/5, 14/15 & 16/17 [SSC CGL 03/12/2022 (1st Shift)]
The LCM of two numbers is 120 and the numbers are in the ratio 3 : 8. The sum of the numbers will be: [SSC CGL 03/12/2022 (3rd Shift)]
The LCM of the two numbers is 56 times their HCF, with the sum of their HCF and LCM being 1710. If one of the two numbers is 240, then what is the other number? [SSC CGL 11/04/2022 (Morning)]
Which is the smallest multiple of 7, which leaves 5 as a remainder in each case, when divided by 8, 9, 12 and 15? [SSC CGL 12/04/2022 (Morning)]
A and B are two prime numbers such that A > B and their LCM is 209. The value of A2 - B is? [SSC CGL 12/04/2022 (Evening)]
What is the greatest four-digit number which on being divided by 6, 7 and 8 leaves 4, 5 and 6 as remainders, respectively? [SSC CGL 18/04/2022 (Afternoon)]
Three numbers are in the ratio If the difference between the greatest number and the smallest number is 33, then HCF of the three numbers is: [SSC CGL Tier II (03/02/2022)]
When 1062, 1134 and 1182 are divided by the greatest number x, the remainder in each case is y. What is the value of (x - y)? [SSC CGL Tier II (15/11/2020)]
Let x be the greatest number which when divided by 955, 1027, 1075, the remainder in each case is the same. Which of the following is NOT a factor of x? [SSC CGL Tier II (16/11/2020)]
The LCM of two numbers x and y is 204 times their HCF. If their HCF is 12 and the difference between the numbers is 60, then x + y = ? [SSC CGL Tier II (13/09/2019)]