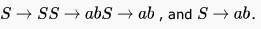Test: Syntax Directed Translation- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Syntax Directed Translation- 1
To evaluate an expression without any embedded function calls
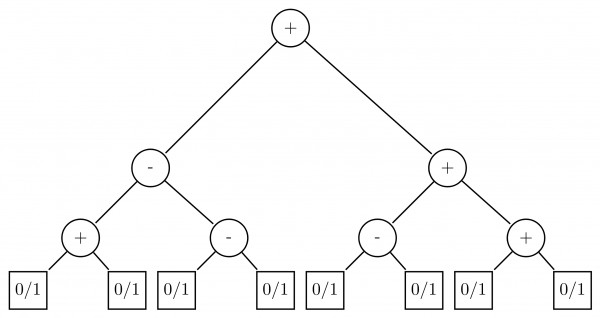
Consider the expression tree shown. Each leaf represents a numerical value, which can either be 0 or 1. Over all possible choices of the values at the leaves, the maximum possible value of the expression represented by the tree is ___.
Which one of the following grammars is free from left recursion?
The number of possible min-heaps containing each value from {1, 2, 3, 4, 5, 6, 7} exactly once is _______.
Which of the following features cannot be captured by context-free grammars?
Consider a grammar with the following productions
The above grammar is:
The grammar whose productions are
-> if id then <stmt>
-> if id then <stmt> else <stmt>
-> id := id
is ambiguous because
In the following grammar
Which of the following is true?
A grammar that is both left and right recursive for a non-terminal, is:
Given the following expression grammar:
Which of the following is true?
Consider the grammar shown below
S → i E t S S’ | a
S’ → e S | ε
E → b
In the predictive parse table, M, of this grammar, the entries M[S’ , e] and M[S’ , $] respectively are
Consider the translation scheme shown below.
Here num is a token that represents an integer and num.val represents the corresponding integer value. For an input string ‘9 + 5 + 2’, this translation scheme will print
Consider the grammar with the following translation rules and E as the start symbol
Compute E.value for the root of the parse tree for the expression:2 # 3 & 5 # 6 & 4
Which of the following grammar rules violate the requirements of an operator grammar? P, Q, R are nonterminals, and r, s, t are terminals.
Consider the following grammar G:
Let Na(ω) and Nb(ω) denote the number of a’s and b’s in a string ω respectively.
Consider the grammar:
For a sentence 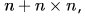 , the handles in the right-sentential form of the reduction are:
, the handles in the right-sentential form of the reduction are:
Consider the following statements about the context free grammar
I. G is ambiguous
II. G produces all strings with equal number of a's and b's
III. G can be accepted by a deterministic PDA
Which combination below expresses all the true statements about ?
Which one of the following grammars generates the language
Consider the grammar with non-terminals N= {S,C,S1} terminals T = {a,b,i,t,e} with S as the start symbol, and the following set of rules:
The grammar is NOT LL(1) because: