Test: Syntax Directed Translation- 2 - Computer Science Engineering (CSE) MCQ
7 Questions MCQ Test - Test: Syntax Directed Translation- 2
Consider the following two statements:
P: Every regular grammar is LL(1)
Q: Every regular set has a LR(1) grammar
Which of the following is TRUE?
Consider the CFG with {S,A,B) as the non-terminal alphabet, {a,b) as the terminal alphabet, S as the start symbol and the following set of production rules:
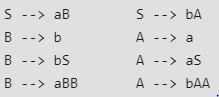
Which of the following strings is generated by the grammar?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the CFG with {S,A,B) as the non-terminal alphabet, {a,b) as the terminal alphabet, S as the start symbol and the following set of production rules:
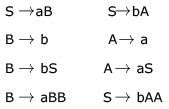
For the string aabbab , how many derivation trees are there?
Which of the following statements are true?
I. Every left-recursive grammar can be converted to a right-recursive grammar and vice-versa
II. All ∈ -productions can be removed from any context-free grammar by suitable transformations
III. The language generated by a context-free grammar all of whose productions are of the form (where ω , is a string of terminals and is a non-terminal), is always regular
IV. The derivation trees of strings generated by a context-free grammar in Chomsky Normal Form are always binary trees
Consider an ambiguous grammar G and its disambiguated version D. Let the language recognized by the two grammars be denoted by L(G) and L(D) respectively. Which one of the following is true?
Consider these three grammars.
Which of the following statements is not true?

















