Test: Regular Expressions & Languages- 2 - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test - Test: Regular Expressions & Languages- 2
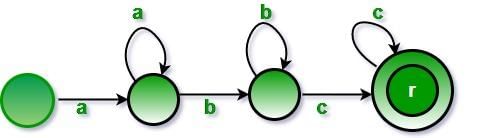
Consider the regular grammar below
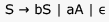
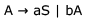
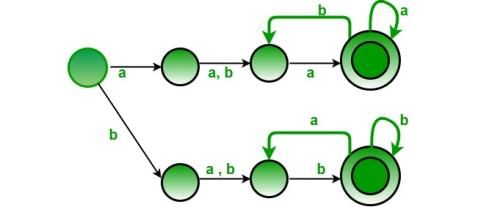
The Myhill-Nerode equivalence classes for the language generated by the grammar are
Consider the alphabet ∑ = {0,1} , the null/empty string λ and the set of strings X0,X1 and X2 generated by the corresponding non-terminals of a regular grammar. X0,X1 and X2 are related as follows.
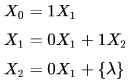
Which one of the following choices precisely represents the strings in X0?
Let L1 and L2 be languages over an alphabet £ such that L1 ⊂ L2. Which of the following is true
Language L1 is defined by the grammar:
Language L2 is defined by the grammar:
Consider the following statements:
Which one of the following is TRUE?
Choose the correct alternatives (More than one may be correct).
Let R1 and R2 be regular sets defined over the alphabet ∑ Then:
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only: Which of the following is the strongest correct statement about a finite language over some finite alphabet ?
Which of the following statements is false?
What can be said about a regular language L over { a } whose minimal finite state automaton has two states?
Consider the following two statements:
Which of the following statement is correct?
Consider the following languages:
Which of the languages are regular?
If s is a string over (0+1)* then let n0(s) denote the number of 0’s in s and n1(s) the number of 1’s in s. Which one of the following languages is not regular ?
Which of the following statements about regular languages is NOT true ?
Let L be a regular language. Consider the constructions on L below:
Which of the constructions could lead to a non-regular language?
Which of the following languages is regular?
Which of the following languages is (are) non-regular?
reads the same forward and backward}
contains an even number of 0's and an even number of 1's}
Which of the following are regular sets?
Let P be a regular language and Q be a context-free language such that (For example, let P be the language represented by the regular expression
Then which of the following is ALWAYS regular?
Given the language which of the following strings are in L*?
Consider the languages Which one of the following represents
Which of the following is/are regular languages?
, is the reverse of string ω
Consider the following three statements:
(i) Intersection of infinitely many regular languages must be regular.
(ii) Every subset of a regular language is regular.
(iii) If L is regular and M is not regular then L.M is necessarily not regular.
Which of the following gives the correct true/false evaluation of the above?
Let B consist of all binary strings beginning with a 1 whose value when converted to decimal is divisible by 7 .
Which one of the following languages over the alphabet 0,1 is regular?
Identify the regular expression which represents the language containing all strings of a's and b's where each string contains at least two b's