Test: Properties of Fluids & Turbulent Flow in Pipes - 1 - Mechanical Engineering MCQ
20 Questions MCQ Test - Test: Properties of Fluids & Turbulent Flow in Pipes - 1
Assertion (A): In a fluid, the rate of deformation is far more important than the total deformation it self.
Reason (R): A fluid continues to deform so long as the external forces are applied.
Reason (R): A fluid continues to deform so long as the external forces are applied.
While water passes through a given pipe at mean velocity V the flow isfound to change from laminar to turbulent. If another fluid of specificgravity 0.8 and coefficient of viscosity 20% of that of water, is passed through the same pipe, the transition of flow from laminar to turbulentis expected if the flow velocity is:
Flow takes place and Reynolds Number of 1500 in two different pipes with relative roughness of 0.001 and 0.002. The friction factor
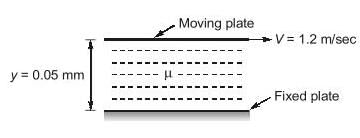
A plate 0.05 mm distant from a fixed plate moves at 1.2 m/sec and requires a shear stress of 2.2 N/m2 to maintain this velocity. Find the viscosity of the fluid between the plates. ___ x 10-5
The shear stress developed in lubricating oil, of viscosity 9.81poise, filled between two parallel plates 1 cm apart and moving with relative velocity of 2 m/s is:
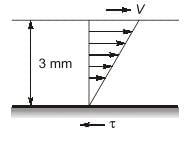
The space between two parallel plates kept 3 mm apart is filled with an oil of dynamic viscosity 0.2 poise. The shear
stresses on the fixed plate, if the upper one is moving with a velocity of 90 m/min is __ N/m2
An oil of specific gravity 0.9 has viscosity of 0.28 Strokes at 380C.What will be its viscosity in Ns/m2?
Assertion (A): In general, viscosity in liquids increases and ingases it decreases with rise in temperature. Reason (R): Viscosity is caused by inter molecular forces of cohesion and due to transfer of molecular momentum between fluid layers; of which in liquids the former and in gases the later contribute the major part towards viscosity.
The pressure drop in a 100 mm diameter horizontal pipe is 50 kPa overa length of 10m. The shear stress at the pipe wall is:
A cylindrical tank of radius 1.5 m and height 3 m is filled with water. A cube of side 0.5 m and density 900 kg/m³ is placed at the bottom of the tank. The water has a density of 1000 kg/m³. What is the minimum height of water required to just lift the cube off the bottom of the tank?
In a Couette flow setup, the fluid between two parallel plates moves due to the motion of the upper plate. The distance between the plates is 0.05 m, and the velocity of the top plate is 2 m/s. If the viscosity of the fluid is 0.3 Pa-s, what is the shear stress at the bottom plate?
A flat plate of width 2 m is moved with a velocity of 0.02 m/s in the downward direction. If the gap between the plate and the wall is 0.02 m, what is the average velocity of the fluid between the plate and the wall?
A lubricant flows between two concentric cylinders, with an inner cylinder rotating at a speed of 4 m/s. The gap between the cylinders is 1 mm, and the dynamic viscosity of the lubricant is 0.05 Pa-s. What is the frictional resisting force per unit length of the cylinder?
A fluid flows between two parallel plates with a gap of 0.1 m. The top plate moves with a velocity of 2 m/s, and the fluid has a dynamic viscosity of 0.5 Pa-s. What is the force per unit area required to maintain the bottom plate stationary?
A journal bearing has a journal diameter of 80 mm and a bush diameter of 81 mm. The bearing length is 25 mm, and the rotational speed of the journal is 1500 rpm. The viscosity of the lubricant is 0.4 Pa-s. What is the power loss due to friction in the bearing?
A spherical air bubble with a diameter of 0.005 m is immersed in oil with a surface tension of 0.03 N/m. What is the difference in pressure across the air bubble?
A plate of width 1.5 m is moving at 1 m/s in a fluid with viscosity 0.2 Pa-s. The gap between the plate and the stationary wall is 0.1 m. What is the shear stress acting on the plate?
A ball of radius 0.02 m falls under the influence of gravity through a viscous fluid. The terminal velocity of the ball is reached when the gravitational force is balanced by the drag force. If the drag coefficient is 0.5 and the fluid has a viscosity of 0.1 Pa-s, what is the terminal velocity of the ball?
A vertical plate of height 1 m is moved with a velocity of 0.1 m/s in a fluid with a viscosity of 0.4 Pa-s. If the gap between the plate and the wall is 0.05 m, what is the shear stress on the plate?
A water tank is connected to a pipe with a diameter of 0.05 m. The pipe discharges water horizontally with a velocity of 2 m/s. What is the force exerted by the water on the pipe due to the discharge, assuming the density of water is 1000 kg/m³?