Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - JEE MCQ
Test Description
30 Questions MCQ Test - Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1)
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) for JEE 2024 is part of JEE preparation. The Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) questions and answers have been prepared
according to the JEE exam syllabus.The Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) MCQs are made for JEE 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) below.
Solutions of Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) questions in English are available as part of our course for JEE & Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) | 30 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 1
If 100 + x < 41 – 6x < 121 + x then
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 1
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 2
then x is equal to
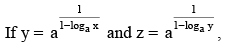then x is equal to | 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 3
The set of real values of x for which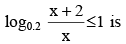 
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 3
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 4
The solution set of |x2 + x| = x2 + x is given by
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 4
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 5
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 6
Find the value(s) of x which satisfy 
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 6
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 7
If x ∈ R, the solution set of the inequation 4–x + 0.5 – 7. 2–x – 4 < 0 is equal to
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 7
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 8
The solution set of the inequality 
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 9
Set of values of x which satisfies 
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 9
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 10
If 3x+2 - 9-1/ x> 0 , then the interval of x can be
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 10
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 11
If log2x + logx2 = 10/3 and log2y + logy2 = 10/3 then the value of x + y (where x ≠ y)
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 11
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 12
the complete solution set of values of x is
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 12
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 13
How many roots of the following equation 3|x| (2- | x |) = 0 has
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 13
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 14
If x satisfies |x2 – 3x + 2| + |x – 1| = x – 3, then
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 14
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 15
If a > 0, then 
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 15
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 16
|2x - 3| < |x + 5|, then x belongs to :
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 16
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 17
The solution set of the equation
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 17
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 18
If a = log1218, b = log2454, then the value of ab + 5(a – b) is
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 18
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 19
If |x - 1|< 5 and |x| >2 . Then x is equal to
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 19
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 20
Greatest negative integral value of x satisfying |4x + 3| = |7x - 1| - 3x - 4|
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 20
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 21
The integral value of x ∈ (–π, π) satisfying the equation |x2 -1+cosx| = |x2 - 1| + |cos x| can be
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 21
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 22
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 22
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 23
The set of values of x satisfying the inequality (x – 1)7 (3 – x)5 (x – 2)4 > 0 is
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 23
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 24
The set of values of x satisfying the inequality 
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 24
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 25
If P and Q are sum and product respectively of all real values of x satisfying the equation 
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 25
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 26
If log2 x + log2 y > 6 , then the least value of (x + y) is :
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 26
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 27
If log2 |4 - 5x| > 2 . Then complete solution set is equal to
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 27
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 28
If log72 = m, then log4928 is equal to
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 28
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 29
Maximum value of log5 (3x + 4y) , if x2 + y2 = 25 is
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 29
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 30
The value of x satisfying 
Detailed Solution for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) - Question 30
Information about Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) Page
In this test you can find the Exam questions for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) solved & explained in the simplest way possible.
Besides giving Questions and answers for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1), EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for JEE
Important Questions for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1)
Find all the important questions for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) at EduRev.Get fully prepared for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) resources.
Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1)
Prepare for the Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) within the JEE exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1)
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Fundamental Of Algebraic Expression MCQ (With Solution) - 3 (Competition Level 1) with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup