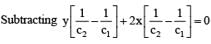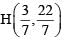JEE Advanced Level Test: Straight Line- 3 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Straight Line- 3
Consider a family of straight lines (x + y) + λ(2x - y + 1) = 0 . Find the equation of the straight line belonging to this family that is farthest from (1,-3)
One side of an equilateral triangle is 3x+4y=7 and its vertex is (1,2). Then the length of the side of the triangle is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the equation of the bisector of the angle between the lines x+2y–11 = 0, 3x–6y–5 = 0 which contains the point (1,–3)
A straight line which make equal intercepts on +ve x and y axes and which is at a distance '1' unit from the origin intersects the straight line y = 2x + 3 + √2 at (x0, y0) then 2x0 + y0
The locus of the image of the point (2, 3) in the line (x -2y +3) + λ (2x -3y + 4) = 0 (λ∈R) is
A straight line L with negative slope passes through the point (8, 2) and cuts the positive coordinate axes at points P and Q. As L varies, the absolute minimum value of OP+OQ is (O is origin)
The number of integral values of m for which the x coordinate of the point of intersection of the lines 3x + 4y = 9 and y = mx + 1 is also an integer is
Area of the parallelogram formed by the lines y = mx, y = mx+ 1, y = nx and y = nx+ 1 equals (m ≠ n)
If the midpoint of sides of a triangle are (a, 0), (0, b) and (-a, -b), then the centroid of the triangle is
The triangle ABC has medians AD, BE, CF. AD lies along the line y = x + 3, BE lies along the line y = 2x + 4, AB has length 60 and angle C = 90°, then the area of ΔABC is
Let A(1, 0), B(0, –2) and P(a, b) be a third point that lies on the straight line 'x - y= 0' such that, |PA + PB| is minimum then the values of |a + b| =
Let A(0, 0), B(3, 0), C(2, 1) then area of the square inscribed in the triangle such that, one side of the square is taken along
Let O(0, 0), A(–1, 1) the point ‘A’ is rotated 60o in anticlockwise sense about origin then the slope of line joining original and the new positions of ‘A’ is
Let y = 2x + c1, y = 2x + c2 meet X-axis at A1, A2 respectively and Y-axis at B1, B2 respectively then the locus of the point of intersection of lines
Let A(2, 3) and B is the image of A with respect to the lines (2x - 3y + 4) + k (x - 2y + 3) = 0 then the locus of B is
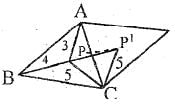
Let 'P' be a point inside the equilateral triangle ABC, PA = 3, PB = 4, PC = 5 then the area of the triangle ABC (in square units)
Let a straight line passing through P(1, 4) with negative slope cuts the coordinate axes at A, B then the area of the triangle OAB when OA + OB is minimum is
The image of the curve with respect to the straight line x + y= 1 is
Let (a, b) lies on obtuse angle bisector of x + 2y + 1 = 0, 2x + y + 1 = 0 then the least value of (a - 1)2 + (b - 2)2 is
Let A(0, 0) and x + y - 1 = 0, 2x + 1 = 0 are the altitude, median from the vertices B, C respectively of ΔABC then the area of the triangle
Let (x - 1)2 + (y - 2)2 = 1/4 then the minimum value of " x + 3y+ 4"
Two vertical poles 20 mts, and 80 mts stand apart on a horizontal plane. The height of the point of intersection of the lines joining the top of each pole to the foot of others (in metres)
A(3, 1), B(13, 6), C(13, 21), D(3, 16) forms a parallelogram, then the y-intercept of the line passing through (1, 0) and dividing the parallelogram into two equal areas
If the straight lines ax + by + p = 0 and x cosa + y sina = p are inclined at an angle p/4 and concurrent with the straight line x sina – y cosa = 0, then the value of a2 +b2 is
Let (1, 2), (3, 8), (4, 1) are three vertices of a parallelogram the sum of all possible x coordinates of the fourth vertex of the parallelogram is
The orthocenter of the triangle formed by the lines x - 7y + 6 = 0, 2x - 5y - 6 = 0 and 7x + y - 8 = 0 is
The equations x = t3 + 9 and 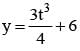 represents a straight line where t is a parameter. Then y-intercept of the line is :
represents a straight line where t is a parameter. Then y-intercept of the line is :
The vertices of triangle ABC are A(–1,–7), B(5, 1) and C(1, 4). The equation of the bisector of the angle ABC of ΔABC is :
y - 1 = m1 x - 3 and y - 3 = m2 (x - 1) are two family straight lines (m1, m2R), at right angles to each other. The locus of their point of intersection is :
The equation of the line passing through the intersection of the lines 3x + 4y = -5, 4x + 6y = 6 and perpendicular to 7x - 5y + 3 = 0 is :



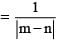 Whre y = mx + 1, x (distance between | | lines) and π/4 (0,3)
Whre y = mx + 1, x (distance between | | lines) and π/4 (0,3)