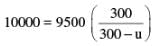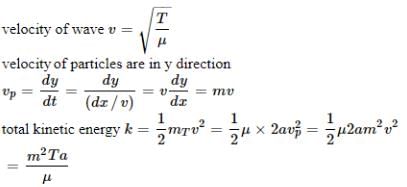Test: Waves - 2 - Grade 8 MCQ
30 Questions MCQ Test - Test: Waves - 2
A plane sound wave is travelling in a medium. In a reference frame A fixed to the medium , its equation is y = a cos(ωt − kx ) . With respect to reference frame B, moving with a constant velocity v in the direction of propagation of the wave, equation of the wave will be
A stationary observer receives sonic oscillations from two tuning forks, one of which approaches and the other recedes with same speed. As this takes place the observer hears the beat frequency of 2 Hz. Find the speed of each tuning fork,(assuming it is very small when compared to sound) if their oscillation frequency is 680 Hz and the velocity of sound in air is 340 m/s.
A sinusoidal wave is generated by moving the end of a string up and down, periodically. The generator must apply the energy at maximum rate when the end of the string attached to generator has X and least power when the end of the string attached to generator has Y. The most suitable option which correctly fills blanks X and Y, is
At t= 0, a transverse wave pulse travelling in the positive x direction with a speed of 2 m/s in a wire is described by the function y = 6/x2 given that x ≠ 0. Transverse velocity of a particle at x = 2 m and t = 2 s is
A stationary observer receives sonic oscillations from two tuning forks, one of which approaches and the other recedes with same speed. As this takes place the observer hears the beat frequency of 2 Hz. Find the speed of each tuning fork,(assuming it is very small when compared to sound) if their oscillation frequency is 680 Hz and the velocity of sound in air is 340 m/s.
In the arrangement shown in figure, the string has a mass of 4.5 g. how much time will it take for a transverse disturbance produced at the floor to reach the pulley. Take g = 10ms-2
A string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Distance between the two points having amplitude 2 mm is:
A 75 cm string fixed at both ends produces resonant frequencies 384 Hz and 288 Hz without there being any other resonant frequency between these two. Wave speed for the string is :
A string of length ℓ is fixed at both ends. It is vibrating in its 3rd overtone with maximum amplitude ‘a’. The amplitude at a distance l /3 from one end is :
A chord attached about an end to a vibrating fork divides it into 6 loops. When its tension is 36N. The tension at which it will vibrate in 4 loops when attached to same tuning fork is:
The figure shows at time t = 0, a rectangular and triangular pulse on a uniform wire are approaching each other. The pulse speed is 0.5 cm/s. The resultant pulse at t = 2 second
is
In a stationary wave that forms as a result of reflection of waves from an obstacle the ratio of the amplitude at an antinode to the amplitude at nodes is n. The fraction of energy reflected is:
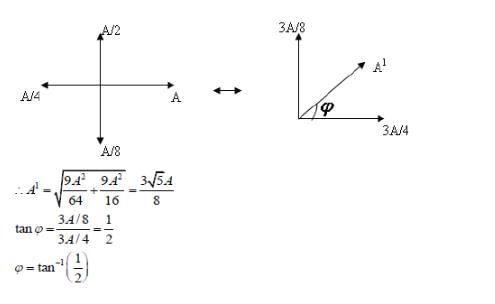
Four waves are described by equations as follow
and their resultant wave is calculated as Y = Y1 + Y2 + Y3 + Y4 such as Y = A1 cos ( ωt − kx + φ ) then………..(symbols have their usual meanings)
A sound wave of frequency 440 Hz is passing through air. An O2 molecule (mass = 5.3 × 10-26 kg) is set in oscillation with an amplitude of 10-6 m. Its speed at the mean position of oscillation is :
A 100 m long rod of density 10.0 x 104 kg/m3 and having Young’s modules Y = 1011 Pa, is clamped at one end. It is hammered at the other free end. The longitudinal pulse goes to right end, gets reflected and again returns to the left end. How much time, the pulse take to go back to initial point.
For a sound wave travelling in air towards +x direction, sinusoidal longitudinal displacement ξ at a certain time is given as a function of x. If Bulk modulus of air is B = 5 × 105 N/m2, the variation of pressure excess will be:
An aluminium wire of length 60cm is joined to a steel wire of length 80 cm and stretched between two fixed supports.
The tension produced is 40 N. The cross – sectional areas of the steel and aluminium wires are 1.0mm2 and 3.0mm2 respectively. The densities of steel and aluminium are 7.8 g / cm3 and 2.6 g / cm3 respectively. The frequency of first overtone of this composite wire with the joint as a node is nearly
Equation of a stationary and a travelling waves are as follows y1 = a sin kx cos ωt and y2 = a sin ( ωt − kx ) . The phase difference between two points in the standing wave ( y1 ) and is φ2 in travelling wave (y2) , then ratio
Figure shown is a graph, at a certain time t, of the displacement function S ( x, t ) of three sound waves 1,2 and 3 as marked on the curves that travel along x-axis through air. If P1, P2 and P3 represent their pressure oscillation amplitudes respectively, then correct relation between them is:
Two sound waves move in the same direction in the same medium. The pressure oscillation amplitudes of the waves are equal but the wave length of the first wave is double that of second. Let the average power transmitted across a cross section by first wave be P1 and that by second wave be P2. Then
Two pulses in a stretched string whose centres are initially 8 cm apart are moving towards each other as shown in figure. The speed of each pulse is 2 cm/s. After 2 s the total energy of the pulses will be
A stretched string of length 1m fixed at both ends, having a mass 5×10−4kg is under a tension of 20N. It is plucked at a point situated at 25 cm from one end. The stretched string could vibrate with a frequency of
A piano wire having a diameter of 0.90 mm is replaced by another wire of the same length and material but with a diameter of 0.93 mm. If the tension of the wire is kept the same, then the percentage change in the frequency of the fundamental tone is nearly
Two sound sources each emitting waves of wavelength λ are fixed a given distance apart and an observer moves from one source to another with velocity u. Then number of beats heard by him
A car is moving towards a high cliff. The driver sounds a horn of frequency f. The reflected sound heard by the driver has frequency 2f. If v is the velocity of sound then the velocity of the car is
A conveyor belt moves to the right with speed v=300 m/min. A pieman puts pies on the belt at a rate of 20 per minute while walking with speed 30 m/min towards a receiver at the other end. The frequency with which they are received by the stationary receiver is :
In the figure shown a source of sound of frequency 510 Hz moves with constant velocity Vs = 20 m / s in the direction shown. The wind is blowing at a constant velocity Vw = 20 m / s towards an observer who is at rest at point B. Corresponding to the sound emitted by the source at initial position A, the frequency detected by the observer is equal to (speed of sound relative to air = 330 m/s)
A whistle producing sound waves of frequencies 9,500 Hz and above is approaching a stationary person with speed u ms-1. The velocity of sound in air is 300 ms-1 . If the person can hear frequencies upto a maximum of 10,000 Hz, The maximum value of u upto which he can hear the whistle is
A police car moving at 22 ms-1 , chases a motorcyclist. The police man sounds his horn at 176 Hz, while both of them move towards a stationary siren of frequency 165 Hz. Calculate the speed of the motorcycle, if it is given that the motor cyclist does not observe any beats. (Velocity of sound is 330 ms −1 )
The wave function of a triangular wave pulse is defined by the relation below at time
t = 0 sec.
The wave pulse is moving in the +X direction in a string having tension T and mass per unit length μ . The total energy present with the wave pulse is




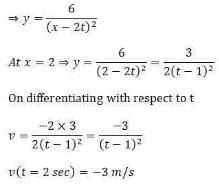
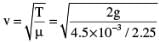 where v is velocity, T is tension in the string and μ is the mass per unit length
where v is velocity, T is tension in the string and μ is the mass per unit length