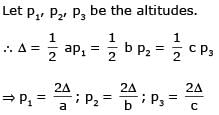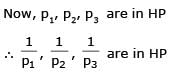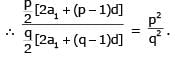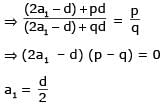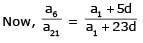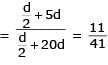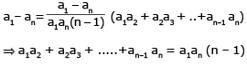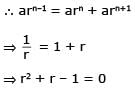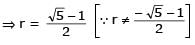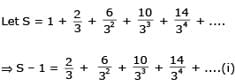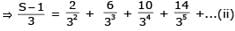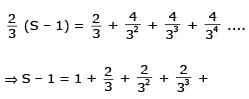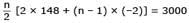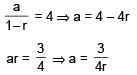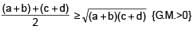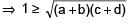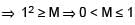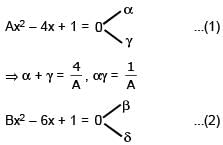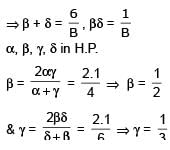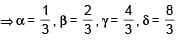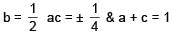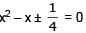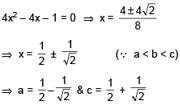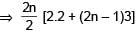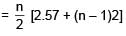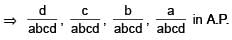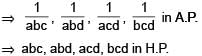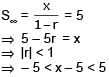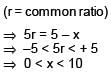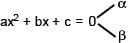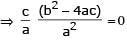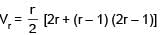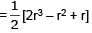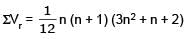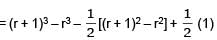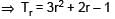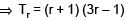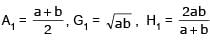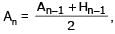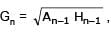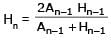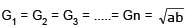Test: JEE Previous Year Questions- Sequence & Series- 1 - JEE MCQ
30 Questions MCQ Test - Test: JEE Previous Year Questions- Sequence & Series- 1
The sum of the series 13 – 23 + 33 – ......+ 93 =
[AIEEE- 2002]
If the sum of an infinite GP is 20 and sum of their square is 100 then common ratio will be =
[AIEEE- 2002]
If the third term of an A.P. is 7 and its 7th term is 2 more than three times of its 3rd term, then sum of its first 20 terms is-
[AIEEE- 2002]
If x1, x2, x3 and y1, y2, y3 are both in G.P. with the same common ratio, then the points (x1, y1), (x2, y2) and (x3, y3)
[AIEEE- 2003]
Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation-
[AIEEE- 2004]
Let Tr be the rth term of an A.P. whose first term is a and common difference is d. If for some positive integers m, n, m ≠ n, Tm = 1/n and Tn = 1/m, then a - d equals-
[AIEEE- 2004]
The sum of the first n terms of the series 12 + 2. 22 + 32 + 2.42 + 52 + 2.62 +..... is 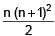 when n is even. When n is odd the sum is-
when n is even. When n is odd the sum is-
[AIEEE- 2004]
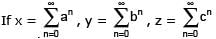 where a, b, c are in A.P. and I a I < 1, l b I < 1, I c I < 1 then x, y, z are in -
where a, b, c are in A.P. and I a I < 1, l b I < 1, I c I < 1 then x, y, z are in -
[AIEEE- 2005]
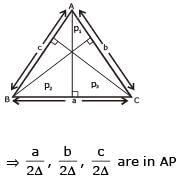
If in a ΔABC, the altitudes from the vertices A, B, C on opposite sides are in H.P., then sin A, sin B, sin C are in
[AIEEE- 2005]
Let a1, a2, a3, ..... be terms of an A.P.
[AIEEE- 2006]
If a1, a2, ..... an are in H.P., then the expression a1a2 + a2a3 +....+ an –1an is equal to –
[AIEEE- 2006]
In a geometric progressionconsisting of positive terms, each term equals the sum of the next two terms. Then the common ratio of this progression equals-
The sum to infinity of the series
[AIEEE 2009]
A person is to count 4500 currency notes. Let an denote the number of notes he counts in the nth minute. If a1 = a2 = .... = a10 = 150 and a10, a11 .... are in an AP with common diferencec –2, then the time taken by him to count all notes is -
[AIEEE 2010]
Statement 1 : The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + ...... ....+(361 + 380 + 400) is 8000.
Statement 2 : 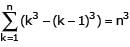 for any natural number n.
for any natural number n.
[AIEEE- 2012]
If 100 times the 100th term of an AP with non zero common difference equals the 50 times its 50 th term, then the 150th term of this AP is:
[AIEEE 2012]
Consider an infinite geometric series with first term a and common ratio r. If the sum is 4 and the second term is 3/4, then
[JEE 2000,]
If a, b, c, d are positive real numbers such that a + b + c + d = 2, then M = (a + b) (c + d) satisifes the relation :
Given that α,γ are roots of the equation, Ax2–4x+1 = 0 and β, δ the roots of the equation, Bx2 – 6x + 1 = 0, find values of A and B, such that 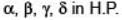
[REE 2000, 5]
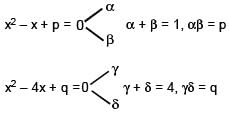
Le α, β be the roots of x2 – x + p = 0 and γ, δ the roots of x2 – 4x + q = 0. If α, β, γ, δ are in G.P., then the integral values of p and q respectively, are
Suppose a, b, c are in A.P. and a2, b2, c2 are in G.P. if a < b < c and a + b + c = 3/2, then the value of a is
[JEE 2002 ]
If the sum of the first 2n terms of the A.P. 2, 5, 8,... ..........is equal to the sum of the first n terms of the A.P. 57, 59, 61,......., then n equals
Let the positive numbers a, b, c, d be in A.P. Then abc, abd, acd, bcd are
[JEE 2001, (Scr.)]
The first term of an infinite geometric progression is x and its sum is 5. Then
[JEE 2004 (Scr.)]
In the quadratic equati on ax2 + bx + c = 0, If Δ = b2 – 4ac and α + β, α2 + β2, α3+ β3, are in G.P. where α , β are the roots of ax2 + bx + c = 0, then
[JEE 2005 (Scr.)]
Let Vr d enote the sum of first r terms of an arithmetic progression (A.P.) whose first term is r and the common difference is (2r – 1). Let Tr = V r + 1 – Vr – 2 and Qr = Tr + 1 – Tr for r = 1, 2,.....
The sum V1 + V2 + ....... + Vn is
Let Vr denote the sum of first r terms of an arithmetic progression (A.P.) whose first term is r and the common difference is (2r – 1). Let Tr = V r + 1 – Vr – 2 and Qr = Tr + 1 – Tr for r = 1, 2,.....
Tr is always
Le t Vr d enote the sum of first r terms of an arithmetic progression (A.P.) whose first term is r and the common difference is (2r – 1). Let Tr = V r + 1 – Vr – 2 and Qr = Tr + 1 – Tr for r = 1, 2,.....
Which one of the following is a correct statement ?
Let A1, G1, H1 denote the arithmetic, geometric and harmoni c means, respectively, of two distinct positive numbers. For n ≥ 2, Let An – 1 and Hn – 1 have arithmetic, geometric and harmonic means as An, Gn, Hn respectively
Which one of the following statements is correct ?
G1,G2,…,Gn are said to be n geometric means between a and b if a,G1,…Gn,b is


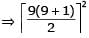 - 2.23 (1 + 23 + 33 +43)
- 2.23 (1 + 23 + 33 +43)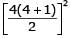

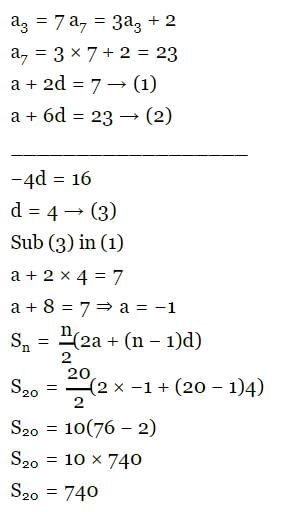

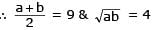
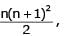 if n is even.
if n is even.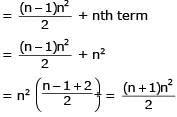
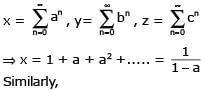
 .........(ii)
.........(ii)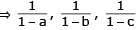 are in AP.
are in AP.