MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - JEE MCQ
Test Description
18 Questions MCQ Test - MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1)
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) for JEE 2024 is part of JEE preparation. The MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) questions and answers have been prepared
according to the JEE exam syllabus.The MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) MCQs are made for JEE 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) below.
Solutions of MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) questions in English are available as part of our course for JEE & MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) | 18 questions in 36 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 1
If cos x + cos y + cos a = 0 and sin x + sin y + sin a = 0, then cot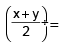 
[AIEEE-2002]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 1
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 2
cos 1°. cos 2°. cos 3°.... cos 179° =
[AIEEE-2002]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 3
Let α and β be such that π < α - β < 3π If sinα + sinβ = -21/65 and cosα + cosβ = -27/65 ,then the value of cos α - β/2 is
[AIEEE-2004]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 3
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 4
[AIEEE-2009]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 4
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 5
Let cos ( α + β ) = 4/5 and let sin ( α - β ) = 5/13 , where 
[AIEEE-2010]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 5
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 6
If A = sin2x + cos4x, then for all real x :
[AIEEE-2011]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 6
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 7
In a ΔPQR if 3 sin P + 4 cos Q = 6 and 4 sin Q + 3 cos P = 1, then the angle R is equal to :
[AIEEE-2012]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 7
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 8
Let f(θ) = sin θ (sin θ + sin 3θ). Then f(θ) :
[JEE 2000 (Scr.)]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 8
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 9
Find the maximum and minimum values of 27cos 2x . 81sin 2x.
[JEE 2000 (Mains), 3]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 9
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 10
Find the smallest positive values of x & y satisfying, x–y= π/4 , cot x+cot y=2.
[REE 2000, 3]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 10
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 11
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 12
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 13
In an equilateral triangle, 3 coins of radii 1 unit each are kept so that they touch each other and also the sides of the triangle. Area of the triangle is
[JEE 2005 (Scr.)]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 13
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 14
Let θ ∈ (0, π/4) and t1 =(tan θ)tan θ, t2 =(tan θ)cot θ, t3 = (cot θ)tan θ, t4 = (cot θ)cot θ, then
[JEE 2006, 3]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 14
*Multiple options can be correct
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 15
One or more than one is/are correct : [Q.7 (a) & (b)]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 15
*Multiple options can be correct
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 16
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 17
The maximum value of the expression
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 17
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 18
The positive integer value of n > 3 satisfying the equation 
[JEE 2011]
Detailed Solution for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) - Question 18
Information about MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) Page
In this test you can find the Exam questions for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) solved & explained in the simplest way possible.
Besides giving Questions and answers for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1), EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for JEE
Important Questions for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1)
Find all the important questions for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) at EduRev.Get fully prepared for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) resources.
MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1)
Prepare for the MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) within the JEE exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1)
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ (Previous Year Questions) - Trigonometry Ratio (Competition Level 1) with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup