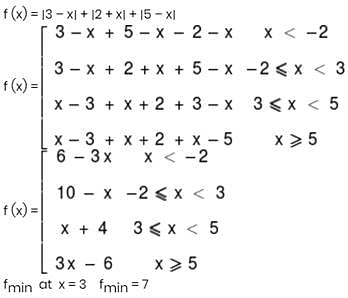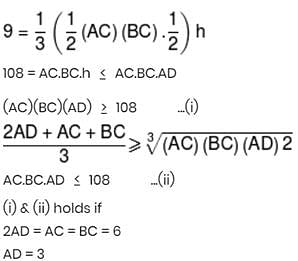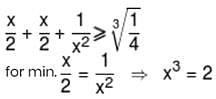All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  JEE Main Maths Test- 9 - JEE MCQ

JEE Main Maths Test- 9 - JEE MCQ


Test Description

25 Questions MCQ Test - JEE Main Maths Test- 9

JEE Main Maths Test- 9 for JEE 2024 is part of JEE preparation. The JEE Main Maths Test- 9 questions and answers have been prepared according to the JEE exam syllabus.The JEE Main Maths Test- 9 MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for JEE Main Maths Test- 9 below.
Solutions of JEE Main Maths Test- 9 questions in English are available as part of our course for JEE & JEE Main Maths Test- 9 solutions in Hindi for JEE course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt JEE Main Maths Test- 9 | 25 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
JEE Main Maths Test- 9 - Question 1
Save

Detailed Solution for JEE Main Maths Test- 9 - Question 1

√3 sin(π/6+h) - cos( π/6+h)

2(√3/2 sin(π/6+h) - 1/2 cos( π/6+h))

2(cos(π/6) sin(π/6+h) - sin(π/6) cos( π/6+h))

2sin(π/6+h -π/6)

2 sin (h)

similarly in the denominator (this next step is not entirely necessary but I think it makes it eaiser)

(√3 cos(h) - sin(h))

2(cos(h+π/6))

lim h-->0 4 sin (h)/2√3 h cos(h+π/6)

(2/√3) (sin h / h)(1/cos h+π/6)

lim h-->0 (sin h / h) = 1

lim h-->0 (1/cos h+π/6) = sec(π/6) = 2/√3

(2/√3)2 = 4/3

JEE Main Maths Test- 9 - Question 2
Save

1 Crore+ students have signed up on EduRev. Have you? Download the App
JEE Main Maths Test- 9 - Question 3
Save

JEE Main Maths Test- 9 - Question 4
Save

JEE Main Maths Test- 9 - Question 5
Save

Detailed Solution for JEE Main Maths Test- 9 - Question 5

lim(x----∞) [x*x(2-3/x)(3-4/x)]/[x*x(4-5/x)(5-6/x)]
= (2*3)/(4*5)
= 6/20
= 3/10

JEE Main Maths Test- 9 - Question 6
Save

................................................ equals
JEE Main Maths Test- 9 - Question 7
Save

If f(a) = 2, f`(a) = 1, g(a) = –1, g`(a) = 2, then value of

Detailed Solution for JEE Main Maths Test- 9 - Question 7

JEE Main Maths Test- 9 - Question 8
Save

The vertices of a triangle ABC are (2,1),(5,2) and (3,4)respectively. The circumcentre is the point
JEE Main Maths Test- 9 - Question 9
Save

If A and B are the points (–3,4) & (2,1). Then the co-ordinates of point C on AB produced such that AC = 2 BC are
JEE Main Maths Test- 9 - Question 10
Save

The equation of the line passing through the intersection of x - √3 y + √3 - 1 = 0 and x y–2 = 0 and
making an angle of 150 with the first line is
JEE Main Maths Test- 9 - Question 11
Save

If 2x2 + λxy + 2y2 +(λ - 4)x + 6y - 5 = 0is the equation of a circle, then its radius is
Detailed Solution for JEE Main Maths Test- 9 - Question 11

JEE Main Maths Test- 9 - Question 12
Save

Equation of circles which pass through the points (1,–2) and (3,–4) and touch the x-axis is
JEE Main Maths Test- 9 - Question 13
Save

The circle whose centre is on the x-axis and the line 4x–3y–12 = 0 and whose radius is the distance
between the line 4x–3y–32 = 0 and 4x–3y–12 = 0 has equation
JEE Main Maths Test- 9 - Question 14
Save

Equation of the circle whose radius is 5 and which touches externally the circle x2 + y2 -2x - 4y - 20 = 0 at
the point (5,5) is
JEE Main Maths Test- 9 - Question 15
Save

The number of integral values of  for λ which  x2 + y2 +λx + (1 - λ) y + 5 = 0is the equation of a
circle whose radius cannot exceed 5 is
JEE Main Maths Test- 9 - Question 16
Save

The angle at which the circle x2 + y2 = 16 can be seen from the point (8,0) is
JEE Main Maths Test- 9 - Question 17
Save

The slope of the tangent at the point (h,h) of the circle  x2 + y2  = a2is
JEE Main Maths Test- 9 - Question 18
Save

If f (x) = [x sin p x] { where [x] denotes greatest integer function}, then f (x) is
JEE Main Maths Test- 9 - Question 19
Save

The equation of the locus of the mid-points of the chords of the circle 4x2 + 4y2 - 12x + 4y +1 = 0that subtend an anlge of 2π / 3 at its centre is
JEE Main Maths Test- 9 - Question 20
Save

The distance of the point (1,2) from the radical axis of the circles x2 + y2 +6x - 16 = 0 and x2 + y2 -2x + 6y = 0  is
*Answer can only contain numeric values
JEE Main Maths Test- 9 - Question 21
Save

Let f(x) be a twice-differentiable function and f''(0) = 2. Then evaluate. 

Detailed Solution for JEE Main Maths Test- 9 - Question 21

*Answer can only contain numeric values
JEE Main Maths Test- 9 - Question 22
Save

The minimum value of  f(x) = ∣3 - x∣ +  ∣2 + x∣ + ∣5 - x∣  is:

Detailed Solution for JEE Main Maths Test- 9 - Question 22

*Answer can only contain numeric values
JEE Main Maths Test- 9 - Question 23
Save

If m is the slope of common tangent of y = x2 – x + 1 & y = x2 – 3x + 1, then |m| is 

Detailed Solution for JEE Main Maths Test- 9 - Question 23

Let point on curve y = x2 – x + 1 be
(x1,x21 – x1 + 1)
∴ Tangent is (y – x21 + x1 – 1) = (2x1 – 1)(x – x1) 
⇒ L1  : y = (2x1 – 1)x – x12 + 1
Let point on curve y = x2 – 3x +1 be (x2, x22 – 3x2 + 1)
∴ Tangent is  (y – x22 + 3x2 – 4) = (2x2 – 3)(x – x2)
⇒ L2 :  y = (2x2 – 3)x – x22 + 1
For common tangent, L1 & L2 are same.
⇒ –x12 + 1 = –x22 + 1
⇒ x1 = ±x2
& 2x1 – 1 = 2x2 – 3
x1 = x2 gives –1 = –3 (rejected)
x1 = –x2 gives x1 = – 1/2, x2 = 1/2
⇒ m = –2.

*Answer can only contain numeric values
JEE Main Maths Test- 9 - Question 24
Save

The volume of a tetrahedron DABC is 9 cubic units. If ∠ACB = π/6 and 2AD + AC + BC = 18, then  the length AD is

Detailed Solution for JEE Main Maths Test- 9 - Question 24

*Answer can only contain numeric values
JEE Main Maths Test- 9 - Question 25
Save

If expression x + 1/x2 (x > 0) attains its minimum value at x = α, then α3 is

Detailed Solution for JEE Main Maths Test- 9 - Question 25

Information about JEE Main Maths Test- 9 Page
In this test you can find the Exam questions for JEE Main Maths Test- 9 solved & explained in the simplest way possible. Besides giving Questions and answers for JEE Main Maths Test- 9, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for JEE Main Maths Test- 9

Find all the important questions for JEE Main Maths Test- 9 at EduRev.Get fully prepared for JEE Main Maths Test- 9 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the JEE Main Maths Test- 9 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of JEE Main Maths Test- 9 resources.

JEE Main Maths Test- 9 MCQs with Answers

Prepare for the JEE Main Maths Test- 9 within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for JEE Main Maths Test- 9

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace JEE Main Maths Test- 9 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup