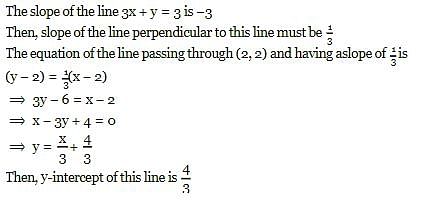All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  JEE Main Maths Test- 11 - JEE MCQ

JEE Main Maths Test- 11 - JEE MCQ


Test Description

30 Questions MCQ Test - JEE Main Maths Test- 11

JEE Main Maths Test- 11 for JEE 2024 is part of JEE preparation. The JEE Main Maths Test- 11 questions and answers have been prepared according to the JEE exam syllabus.The JEE Main Maths Test- 11 MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for JEE Main Maths Test- 11 below.
Solutions of JEE Main Maths Test- 11 questions in English are available as part of our course for JEE & JEE Main Maths Test- 11 solutions in Hindi for JEE course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt JEE Main Maths Test- 11 | 30 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
JEE Main Maths Test- 11 - Question 1
Save

A point P on y-axis is equidistant from the points A(–5,4) and B(3,–2). Its co-ordinates are

JEE Main Maths Test- 11 - Question 2
Save

If the point P(x,y) be equidistant from the points A(a b, b–a) and B(a–b,a b), then

Detailed Solution for JEE Main Maths Test- 11 - Question 2
PA=PB
take square both side 
PA^2=PB^2

now use distance
formula ,
{x-(a+b)}^2+{y-(b-a)}^2={x-(a-b)}^2+{y-(a+b)}^2

=>x^2+(a+b)^2-2x(a+b)+y^2+(b-a)^2-2y(b-a)y=x^2+(a-b)^2-2x(a-b)+y^2+(a+b)^2-2y(a+b)

=>2x(a-b)-2x(a+b)=2y(b-a)-2y(a+b)

=>2x{a-b-a-b}=2y{b-a-a-b}

=>2x(-2b)=2y(-2a)

=>bx=ay 
1 Crore+ students have signed up on EduRev. Have you? Download the App
JEE Main Maths Test- 11 - Question 3
Save

The points (0,8/3),(1,3) and (82,30) are the vertices of

JEE Main Maths Test- 11 - Question 4
Save

P(3,1),Q(6,5) and R(x,y) are three points such that the angle PRQ is a right angle and the area of
RPQ= 7, then the number of such point R is
JEE Main Maths Test- 11 - Question 5
Save

Determine the ratio in which the line 3x + 4y - 9 = 0 divides the line segment joining the points (1,3) and (2,7).
JEE Main Maths Test- 11 - Question 6
Save
Given four lines with equations x+2y–3 = 0, 3x+4y–7 = 0, 2x+3y–4 = 0, 4x+5y–6 = 0, then
JEE Main Maths Test- 11 - Question 7
Save

......PS be the median of the triangle with vertices P(2,2), Q(6,–1) and R(7,3). The equation of the line passing through (1,–1) and parallel to PS is
JEE Main Maths Test- 11 - Question 8
Save
The line 4x+y = cuts the axis of co-ordinates at A and B. If C is the foot of perpendicular drawn from origin O, then AC : CB =
JEE Main Maths Test- 11 - Question 9
Save
Points on the line x+y = 4 that lie at a unit distance from the line 4x+3y–10 = 0 are
JEE Main Maths Test- 11 - Question 10
Save

A line passes through (2,2) and is perpendicular to the line 3x+y = 3. Its y intercept is
Detailed Solution for JEE Main Maths Test- 11 - Question 10

JEE Main Maths Test- 11 - Question 11
Save
The four lines axby c=0 enclose a
JEE Main Maths Test- 11 - Question 12
Save
The reflection of the point(4,–13) in the line 5x+y+6= 0 is
JEE Main Maths Test- 11 - Question 13
Save
The equation of the bisector of the acute angle between the lines 3x–4y+7 = 0 and 12x+5y–2 = 0 is
JEE Main Maths Test- 11 - Question 14
Save
The vertices of a triangle ABC are (1,1), (4,–2) and (5,5) respectively. Then equation of perpendicular dropped from C to the internal bisector of angle A is
JEE Main Maths Test- 11 - Question 15
Save
A line is such that its segements between the straight lines 5x–y = 4 and 3x+4y–4 = 0 is bisected at the point (1,5). Its equation is
JEE Main Maths Test- 11 - Question 16
Save

The radius of the circle whose centre is on y-axis and which passes through the points (5,2) and (7,–4) is
JEE Main Maths Test- 11 - Question 17
Save
Two circles and 0 are such that they
Detailed Solution for JEE Main Maths Test- 11 - Question 17
These are the equation of two circles.The best way to find out whether two circles touches or cuts or do not intersect is to find out the distance between their centres.If this distance is greater than the sum of their radii they don't touch,if equal to sum of radii they just touch, and if less than sum of radii then intersect at two points. If distance is zero then they are concentric.
JEE Main Maths Test- 11 - Question 18
Save
3x+4y–7 = 0 is common tangent at (1,1) to two equal circles of radius 5. Their centres are the points
JEE Main Maths Test- 11 - Question 19
Save

The points (2,3),(0,2),(4,5)and (0,c) are concyclic if the value of c is
JEE Main Maths Test- 11 - Question 20
Save
Equation of the diameter of the circle  which passes through the origin is
JEE Main Maths Test- 11 - Question 21
Save
Which of the following lines is a normal to the circle
JEE Main Maths Test- 11 - Question 22
Save
The equation represents
JEE Main Maths Test- 11 - Question 23
Save

The coordinates of the point on the circle x2+y2-12x-4y+30=0 which is the farthest from the origin are
Detailed Solution for JEE Main Maths Test- 11 - Question 23
Centre of the given circle is - (-12/2) , - ( -4/2)
This means (6,2) is the centre of the circle. 
The farthest point from the origin on the circle has to be the far end of diameter got by joining (0,0) and (6,2)
Equation of line joining these two points is by two point formula
We have x = 3 y 
The point of intersection of this line and circle is got by solving these two
We get points (3,1) and (9,3)
Hence required farthest is (9,3)
JEE Main Maths Test- 11 - Question 24
Save
The angle between two tangents from the origin to the circle is
JEE Main Maths Test- 11 - Question 25
Save
The number of tangents that can be drawn from the point (8,6) to the circle is
JEE Main Maths Test- 11 - Question 26
Save
The equation of the common tangent to the circle , at their point of contact is
JEE Main Maths Test- 11 - Question 27
Save
The intercepts made by the circle on the x-axis and y-axis are respectively
JEE Main Maths Test- 11 - Question 28
Save
The circle touches x-axis, then c =
JEE Main Maths Test- 11 - Question 29
Save
The equation of the passing through the intersection of the circles and having its centre on the line y = x is
JEE Main Maths Test- 11 - Question 30
Save

The vertex A of a triangle ABC is the point (-2, 3) whereas the line perpendicular to the sides AB and AC are x – y – 4 = 0 and 2x – y – 5 = 0 respectively. The right bisectors of sides meet at P(3/2 , 5/2) . Then the equation of the median of side BC is
Information about JEE Main Maths Test- 11 Page
In this test you can find the Exam questions for JEE Main Maths Test- 11 solved & explained in the simplest way possible. Besides giving Questions and answers for JEE Main Maths Test- 11, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for JEE Main Maths Test- 11

Find all the important questions for JEE Main Maths Test- 11 at EduRev.Get fully prepared for JEE Main Maths Test- 11 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the JEE Main Maths Test- 11 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of JEE Main Maths Test- 11 resources.

JEE Main Maths Test- 11 MCQs with Answers

Prepare for the JEE Main Maths Test- 11 within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for JEE Main Maths Test- 11

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace JEE Main Maths Test- 11 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup