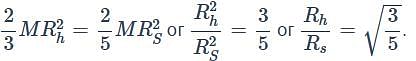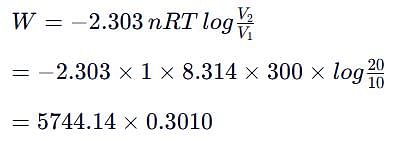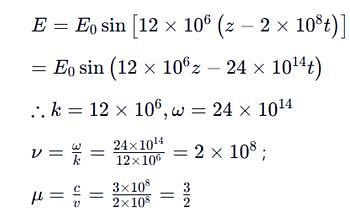JEE Main Physics Test- 2 - JEE MCQ
25 Questions MCQ Test - JEE Main Physics Test- 2
A capillary tube of radius 1 mm is 10 cm long. What maximum height of water it can hold if it is immersed in water upto 5 cm and then taken out of it? (Surface Tension of water = 98 dynes/cm)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Ice floats in water contained in a vessel. When whole ice has melted, water temp. falls from 10°C to 3°C. The water level will
The equation of two simple harmonic motions are given by y1 = 10sin(3πt + π/8) & y2 = 5(cos23πt/2 − sin2πt/2).
The amplitudes are in the ratio of
Two soap bubbles of radii 4 mm & 6 mm are kept in contact. What is radius of curvature at the junction of bubbles.
The time period of a simple pendulum with effective length equal to the radius of Earth (R) will be (g is acceleration due to gravity at the surface of earth)
For the wave represented by the equation y = 3 cos π(100t − x) cm the wave velocity and the maximum particle velocity are
Figure shows a capillary tube of radius r dipped into water. If the atmospheric pressure is P0, the pressure at point A is
Ultrasonic waves emitted by dolphins have a frequency of 250 kHz. Their wavelength in water is nearly
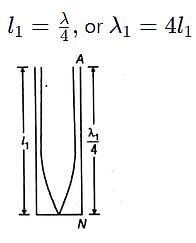
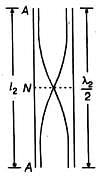
An organ pipe P1 closed at one end vibrating in its first harmonic and another pipe P2 open at both ends vibrating in its third harmonic are in resonance with a given tuning fork. The ratio of the length of P1 to that of P2 is
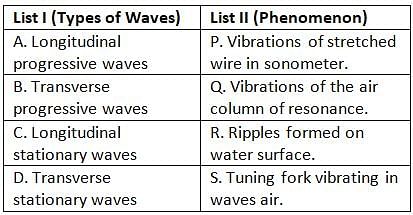
Match list I & list II & select the correct answer given below
Consider the following statements-
In a stationary wave
1. All the particles perform simple harmonic motion with a frequency which is four times that of the two component waves.
2. Particles on the opposite sides of a node vibrate with a phase difference of π.
3. The amplitude of vibration of a particle at an antinode is equal to that of either component wave.
4. All the particles between two adjacent nodes vibrate in phase.
Of these statements-
The centre of a wheel rolling on a plane surface moves with a speed V0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
Three identical rods, each of length l, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing through a corner and perpendicular to the plane of the triangle is
The velocity of a solid sphere after rolling down an inclined plane of height h, from rest, without sliding is
A particle of mass m is moving in a plane along a circular path of radius r. Its angular momentum about the axis of rotation is L. The centripetal force on the particle is
A solid sphere rolls without slipping and presses a spring of spring constant ‘K’ as in fig. at the moment shown a spring was in relaxed state then the maximum compression in the spring will be
A wheel of M. I.(Moment of inertia) 5 x 10-3 kg m2 is making 10 revolution per second. It is stopped in 20 Second. Then angular retardation is
We have two sphere one of which is hollow and the other is solid. They have identical masses and moment of inertia about their respective diameter. The ratio of their radii is
The moment of inertia of a body about a given axis is 1.2 kg-m2. Initially, the body is at rest. In order to produce a rotational KE of 1500 J, an angular acceleration of 25 rad/s2 must be applied about that axis for a duration of :
One mole of an ideal gas expands at a constant temperature of 300 K from an initial volume of 10 litres to a final volume of 20 litres. The work done (in J) in expanding the gas is
(R = 8.31 J/mole-K) (log 2 = 0.3010)
Time taken (in s) by a 836 W heater to heat one litre of water from 10°C to 40°C is :-
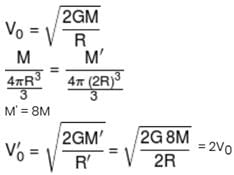
The escape velocity from a planet is v0. The escape velocity from a planet having twice the radius but same density is nv0 then n is :-
For an EMwaves, E = E0 sin (12 × 106 [z – 2 × 108t]) In a medium, it's refractive index is P/2 then P is


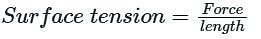
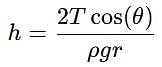
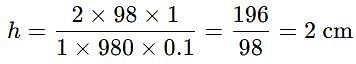
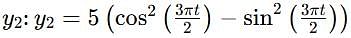 This equation uses trigonometric identities. Recognize that the expression within the parentheses is a standard trigonometric identity: cos2A − sin2A = cos2A. Applying this identity with
This equation uses trigonometric identities. Recognize that the expression within the parentheses is a standard trigonometric identity: cos2A − sin2A = cos2A. Applying this identity with
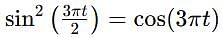 Thus, the equation becomes: y2 = 5cos(3πt) Here, the amplitude is 5.
Thus, the equation becomes: y2 = 5cos(3πt) Here, the amplitude is 5.
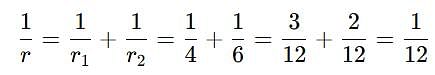
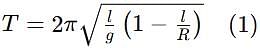
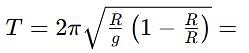
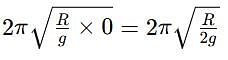
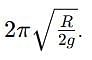
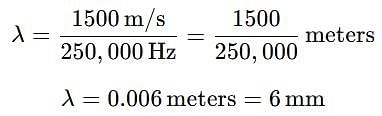
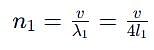
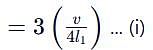
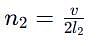
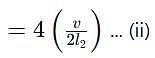
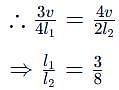
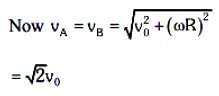
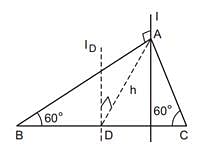
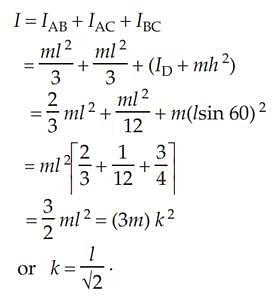
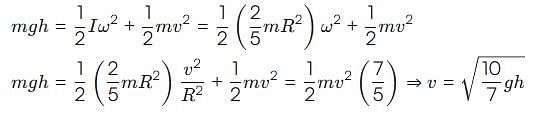
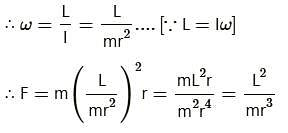
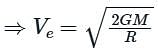
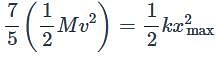
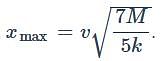
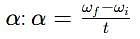
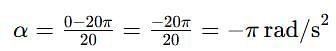
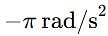 . This negative sign indicates that it is a retardation (or deceleration) since the wheel is slowing down.
. This negative sign indicates that it is a retardation (or deceleration) since the wheel is slowing down.