Test: Even And Odds- 1 - GMAT MCQ
25 Questions MCQ Test - Test: Even And Odds- 1
If x is an integer, is x/2 an even integer?
1) x is divisible by 2
2) x is divisible by 4
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the ratio of number of odd integers to the number of even integers between -10.5 and 10.5?
If m is an integer, is m odd?
1) m/2 is not an even integer
2) m – 3 is not an even integer
The product of integers x, y, and z is even. Is z even?
1) x/y = z
2) z = xy
The product of the units, tens, and hundreds digits of the positive 3-digit integer x is 42. Is x even?
(1) x is less than 300. ?
(2) The tens digit of x is 7. ?
If m, n, and p are integers, is m+n odd??
(1) m = p2 + 4p + 4
(2) n = p2 + 2m + 1
Is the positive integer p even?
(1) p2 + p is even.
(2) 4p + 2 is even.
If p and q are integers and p + q + p is odd, which of the following must be odd?
If a , b, and c are integers and ab2 / c is a positive even integer, which of the following must be true?
I. ab is even
II. ab > 0
III. c is even?
If k and y are integers, and 10k + y is odd, which of the following must be true?
Each digit in the two-digit number G is halved to form a new two-digit number H. Which of the following could be the sum of G and H? ?
If positive integers x and y are not both odd, which of the following must be even?
If i and j are integers, is i + j even?
1) i < 10
2) i = j
If n is an integer, is n even?
1) n2 – 1 is an odd integer
2) 3n + 4 is an even integer
If x and y are both integers, is xy even?
1) x + y is odd
2) x is even
If x and y are integers, is xy even?
1) x = y + 1
2) x/y is an even integer
Is p2 an odd integer?
1) p is an odd integer
2) √p is an odd integer
If x and y are prime integers and x < y, which of the following cannot be true??
If x and y are positive integers, is the product xy even?
1) 5x - 4y is even
2) 6x + 7y is even
If x and y are integers, is x (y + 1) an even number?
1) x and y are prime numbers.
2) y > 7 ?
For all positive integers m, (m) = 3m when m is odd and (m) = (1⁄2) m when m is even, which of the following is equivalent to (9)*(6)?
If m and n are integers, is m odd??
1) m + n is odd
2) m + n = n2 + 5
For non-negative integers x, y, and z, is xz odd?
1) xz = odd
2) x = 2y



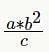 = even > 0 ab2 = c* even = even--> either a is even or b or both.
= even > 0 ab2 = c* even = even--> either a is even or b or both.














