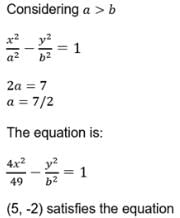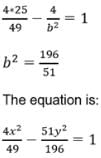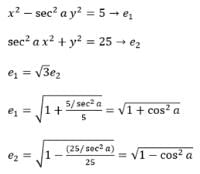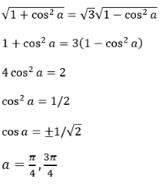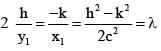WBJEE Mathematics Sample Paper I - JEE MCQ
30 Questions MCQ Test - WBJEE Mathematics Sample Paper I
The equations of the line parallel to X-axis and at a distance of c/2 from the X-axis is:
The line which makes intercepts 3 and 4 on the x and the y axis respectively, has equation
The length of the transverse axis of a hyperbola is 7 and it passes through the point (5, –2). The equation of the hyperbola is
If the eccentricity of the hyperbola x2 – y2 sec2 a = 5 is (√3) times the eccentricity of the ellipse x2 sec2 a + y2 = 25, then a value e of a is
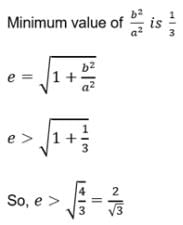
AB is a double ordinate of the hyperbola such that DAOB (where `O' is the origin) is an equilateral triangle, then the eccentricity e of the hyperbola satisfies
The locus of the point of intersection of tangents drawn at the extremities of normal chords to hyperbola xy = c2
The …… of a conic is the chord passing through the focus and perpendicular to the axis.
If the line x + y – 1 = 0 touches the parabola y2 = kx , then the value of k is
Directrix of a parabola is x + y = 2. If it's focus is origin, then latus rectum of the parabola is equal to
There exists a triangle ABC satisfying the conditions
In a ΔABC, (b +c) cos A + (c + a) cos B + (a + b) cos C is equal to
If A and B matrices are of same order and A + B = B + A, this law is known as
For which of the following values of m , is the area of the region bounded by the curve y = x - x2 and the line y = mx equal to 9/2 ?
The area of the region bounded by the parabola (y−2)2 = x−1,the tangent to yhe parabola at the point (2 , 3) and the x – axis is equal to
The area of the loop between the curve y = a sin x and the x – axis and x = 0 , x = π. is
If the three points A(1,6), B(3, –4) and C(x, y) are collinear then the equation satisfying by x and y is
If and θ lies in the second quadrant, then cosθ is equal to
The solutions set of inequation cos–1x < sin–1x is
If sinθ and cosθ are the roots of the equation ax2 – bx + c = 0, then a, b and c satisfy the relation
If A and B are two matrices such that A+B and AB are both defined, then
The equation of the locus of the point of intersection of the straight lines x sin θ + (1 – cos θ) y = a sin θ and x sin θ – (1 + cos θ) y + a sin θ = 0 is