JEE Main Practice Test- 27 - JEE MCQ
30 Questions MCQ Test - JEE Main Practice Test- 27
The area bounded by the parabola y2 = 8x, the x-axis and the latus rectum is
If the coefficients of rth, (r+1)th and (r+2)th terms in the binomial expansion of (1+y)m are in A.P., then m and r satisfy the equation
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Given that the function f defined by 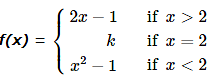 is continuous . Then the value of k is
is continuous . Then the value of k is
The equation of the circle passing thro' (1,0) and (0,1) and having smallest possible radius is
The differential equation of the family of curves y2=4a (x+a) is
The differential equation obtained by eliminating the arbitrary constants a and b from xy = aex + be−x is
The eccentric angles of the extremities of the latus-rectum intersecting positive x-axis of the ellipse ((x2/a2) + (y2/b2) = 1) are given by
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): If M is a n x n matrix with rank n - 1, then M can be made non-singular by changing one element.
Reason(R): An n x n matrix with rank n - 1 has a non-vanishing minor of order n - 1.
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): Solution of
Reason(R): xdx + ydy =
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A):If A and B are two independent events such that
Reason(R):
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): If
Reason(R): We know that
If α , β are the roots of the quadratic equation x2 − (a − 2) x − (a + 1) = 0 , where a is a variable, then the least value of α2 + β2 is
If the parabola y2=4ax passes thro' the point (1,-2), then the tangent at this point is
If log(a + c), log(c - a), log (a - 2b + c) are in A.P., then
If f (x) = {2x - 3, x ≤ 2} {x, x < 2} then f (1) is equal to
If the range of a randon variable X is {0, 1, 2, 3, 4 ...} with , then a =
The ratio in which the line joining the points (a,b,c) and (-a,-c,-b) is divided by the xy-plane is