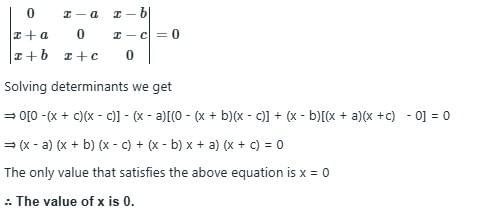WBJEE Maths Test - 3 - JEE MCQ

If a < 0 < b then

The centre and radius of the circle with the segment of the line x+y=1 cut of by the coordinate axes as diameter are

If (a+ib)(c+id)(e+if)(g+ih) = A+iB, then (a²+b²)(c²+d²)(c²+f²)(g²+h²) =

The area bounded by two curves y²=4ax and x²=4ay is

If a, b, c are different and then x =

The orthogonal trajectories of the family y²=4ax+4a² is the family :

The solution of the differential equation x{y d²y/dx² + (dy/dx)²}=y dy/dx is :

If siny=x sin (a+y), (dy/dx)=

The differential of sin⁻¹[(1-x)/(1+x)] w.r.t. √x is equal to

The major axis of an ellipse is three times the minor axis, then the eccentricity is

The eccentricity of ellipse 4x² + 9y² = 36 is

The parametric equations of the hyperbola x²/a² - y²/b² = 1 are

The eccentricity of the conic 9x² - 16y² = 144 is

tan⁻¹(1/4) + tan⁻¹(2/9) is equal to

Let f(x) = tan^-1 {φ(x)}, where φ(x)is monotonically increasing for 0 < x < π/2. Then f(x) is

If A and B are two matrices such that AB = B and BA = A, then A² + B² =

A function f(x) is defined as f (x) = [1 − x²] , − 1 ≤ x ≤ 1 , where [x] denotes the greatest integer not exceeding x. The function f(x) is discontinuous at x = 0 because

A square tank of capacity 250 cubic m has to be dug out. The cost of land is Rs 50 per sq.m. The cost of digging increases with the depth and for the whole tank is 400 (depth)² rupees. The dimensions of the tank for the least total cost are

The normals to the parabola y²=4ax from the point (5a,2a) are

The slope of the normal at the point (at²,2at) of the parabola y²=4ax is