Airforce X Y / Indian Navy SSR Exam > Airforce X Y / Indian Navy SSR Tests > Test: Limits And Continuity : Intuitive Approach - 3 - Airforce X Y / Indian Navy SSR MCQ
Test: Limits And Continuity : Intuitive Approach - 3 - Airforce X Y / Indian Navy SSR MCQ
Test Description
30 Questions MCQ Test - Test: Limits And Continuity : Intuitive Approach - 3
Test: Limits And Continuity : Intuitive Approach - 3 for Airforce X Y / Indian Navy SSR 2024 is part of Airforce X Y / Indian Navy SSR preparation. The Test: Limits And Continuity : Intuitive Approach - 3 questions and answers have been prepared
according to the Airforce X Y / Indian Navy SSR exam syllabus.The Test: Limits And Continuity : Intuitive Approach - 3 MCQs are made for Airforce X Y / Indian Navy SSR 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Limits And Continuity : Intuitive Approach - 3 below.
Solutions of Test: Limits And Continuity : Intuitive Approach - 3 questions in English are available as part of our course for Airforce X Y / Indian Navy SSR & Test: Limits And Continuity : Intuitive Approach - 3 solutions in
Hindi for Airforce X Y / Indian Navy SSR course.
Download more important topics, notes, lectures and mock test series for Airforce X Y / Indian Navy SSR Exam by signing up for free. Attempt Test: Limits And Continuity : Intuitive Approach - 3 | 40 questions in 40 minutes | Mock test for Airforce X Y / Indian Navy SSR preparation | Free important questions MCQ to study for Airforce X Y / Indian Navy SSR Exam | Download free PDF with solutions
Test: Limits And Continuity : Intuitive Approach - 3 - Question 1
If f(x) = (x2 -4)÷(x-2) for x<2, f(x)=4 for x=2 and f(x)=2 for x>2, then f(x) at x = 2 is
Test: Limits And Continuity : Intuitive Approach - 3 - Question 2
f(x) =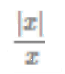 
when x o 0, then f(x) is
when x o 0, then f(x) is| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Limits And Continuity : Intuitive Approach - 3 - Question 3
If 
= i, then which of the following is correct?
= i, then which of the following is correct?
is equal to
Test: Limits And Continuity : Intuitive Approach - 3 - Question 5
If f(x) = x for 0 ≤ x 1/2, f(x) = 1 for x = 1-x for 1/2<x<1 then at x =1/2 the function is
Test: Limits And Continuity : Intuitive Approach - 3 - Question 7
If f(x)=9x÷(x+2) for x<1, f(1)=3, f(x)=(x+3)x-1 for x>1, then in the interval (-3,3) the function is
Test: Limits And Continuity : Intuitive Approach - 3 - Question 9
Function f(x) = K.x-1 for x < 2
= x-k for x ≥ 2
is continuous at x = 2
The value of 'k' is __________.
Test: Limits And Continuity : Intuitive Approach - 3 - Question 13
The points of discontinuity of the function, F(x) = 
are
Test: Limits And Continuity : Intuitive Approach - 3 - Question 16
Find limn→∞(2n-1)2n (2n+1)-1 21-n
Test: Limits And Continuity : Intuitive Approach - 3 - Question 17
Find limn→∞[4n2 + 6n +2] ÷ 4n2
Test: Limits And Continuity : Intuitive Approach - 3 - Question 18
Find limn→∞[xn.(n+1)] ÷ [nx n+1 ]
Test: Limits And Continuity : Intuitive Approach - 3 - Question 19
Find limn→∞[n(n+2)] ÷ (n+1)2
Test: Limits And Continuity : Intuitive Approach - 3 - Question 20
Find limn→∞(n3 +a )[(n+1)3a]-1 (2n+1 +a ) (2n +a)-1
Test: Limits And Continuity : Intuitive Approach - 3 - Question 21
Find limn→∞(n2 +1)[(n+1)2 +1]-1 5n+1 5-n
Test: Limits And Continuity : Intuitive Approach - 3 - Question 22
Find limn→∞nn(n+1)-n-1 ÷ n-1
Test: Limits And Continuity : Intuitive Approach - 3 - Question 23
Find limn→∞2n-1 (10 +n) (9+n)-1 2-n
Test: Limits And Continuity : Intuitive Approach - 3 - Question 24
Find limn→∞(1+n-1)[1+2n)-1]-1
Test: Limits And Continuity : Intuitive Approach - 3 - Question 25
Find limn→∞[nn. (n+1)!] ÷ [n! (n+1)n+1]
Test: Limits And Continuity : Intuitive Approach - 3 - Question 26
Find limn→∞[(n+1)n+1. n-n-1 -(n+1).n-1]-n
Test: Limits And Continuity : Intuitive Approach - 3 - Question 29
Find limn→∞[n!3n+1] ÷[3n(n+1)!]
Test: Limits And Continuity : Intuitive Approach - 3 - Question 30
The value of the limit when x tends to zero of the expression (1+n)1/n is
View more questions
Information about Test: Limits And Continuity : Intuitive Approach - 3 Page
In this test you can find the Exam questions for Test: Limits And Continuity : Intuitive Approach - 3 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Limits And Continuity : Intuitive Approach - 3, EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for Airforce X Y / Indian Navy SSR
Important Questions for Limits And Continuity : Intuitive Approach - 3
Find all the important questions for Limits And Continuity : Intuitive Approach - 3 at EduRev.Get fully prepared for Limits And Continuity : Intuitive Approach - 3 with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Limits And Continuity : Intuitive Approach - 3 syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Limits And Continuity : Intuitive Approach - 3 resources.
Limits And Continuity : Intuitive Approach - 3 MCQs with Answers
Prepare for the Limits And Continuity : Intuitive Approach - 3 within the Airforce X Y / Indian Navy SSR exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Limits And Continuity : Intuitive Approach - 3
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Limits And Continuity : Intuitive Approach - 3 with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup