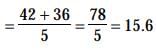Test: Measures Of Central Tendency And Dispersion- 3 - CDS MCQ

If mean = 5, Standard deviation = 2.6, median = 5 and quartile deviatiion = 1.5, then the coefficient of quartile deviation equals.

Which of the following measures of central tendency cannot be calculated by graphical method?

If the relationship between two variables u and v are given by 2u + v + 7 = 0 and if the AM of u is 10, then the AM is v is 

Find at the variance given that the Arithmetic Mean = ( 8 + 4)/2

The price of average whose value can be determined graphically?

If the mean of a frequency distribution is 100 and coefficient of variation is 45% then standard deviation is:

In normal distribution mean, median and mode are 

The mean of the following data is 6.Find the value of 'P'.
x : 2  4  6  10  P+5
f :  3  2  3   1     2

For values lie close to the mean , the standard deviations are

Which of the following statement is true?

 What will be the probable value of mean deviation? When Q³ = 40 and Q¹ = 15

The mean of the first three term is 14 and mean of next two terms is 18. The mean of all five terms is :

 The median of following numbers, which are given is ascending order is 25. Find the value of X.11   13  15  19  (x+2)   (x+4)  30  35  39  46

Geometric Mean of three observations 40, 50 and X is 10. The value of X is 

 If standard deviation of first 'n' natural numbers is 2 then value of 'n' is 

For data on frequency distribution of weights:70, 73, 49, 57, 44, 56, 71, 65, 62, 60, 50, 55, 49, 63 and 45 If we assume class length as 5, the number of class intervals would be 

The point of intersection of the "less than" and "more than" ogives correspond to 

If sum of squares of the values = 3390, N = 30 and standard deviation = 7, find out the mean.

 Which of the following measures of dispersion is used for calculating the consistency between two series?

 If the mode of a data is 18 and mean is 24, then median is _________.

The standard deviation of the weights (in kg) of the students of a class of 50 students was calculated to be 4.5 kg. Later on it was found that due to some fault in weighing machine, the weight of each student was under measured by 0.5 kg. The Correct standard deviation of the weight will be:

 The mean salary of a group of 50 persons is Rs. 5,850. Later on it is discovered that the salary of one employee has been wrongly taken as Rs.8,000 instead of Rs.7,800. The corrected mean salary is 

 For Normal distribution the relation between quartile deviation (Q.D) and standard deviation (S.D) is 

The average age of a group of 10 students was 20 years. The average age increased by two years when two new students joined the group. What is the average age of the two new students who joined the group?

 The standard deviation is independent of change of 

Coefficient of Standard deviation is equal to 

 The mode of the numbers 7, 7, 7, 9, 10, 11, 11, 11, 12, is