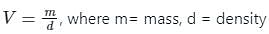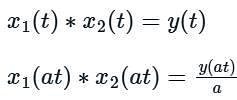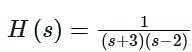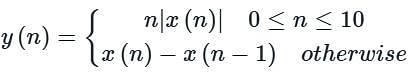Test: Properties of Systems - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Properties of Systems
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
y[t]= ∫x[t],t ranges from 0 to t. Is the system a memoryless one?
y(t) = x(t)2. Is y(t) = sqrt(x(t)) the inverse of the first system?
Given the systems (i) y(n) = n x(n) and (ii) y(n) = ex(n)
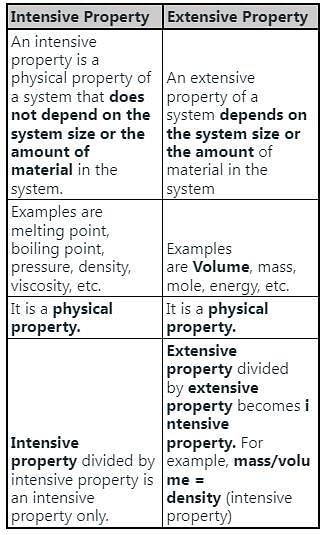
Specific enthalpy is an ________ of a system and its unit is ________.
What is the following type of system called? y[n] = x[n] + y[n-1].
Which property of delta function indicates the equality between the area under the product of function with shifted impulse and the value of function located at unit impulse instant ?
For what value of k, will the following system be time invariant?
y(t) = x(t) + x(kt) – x(2t) + x(t-1)
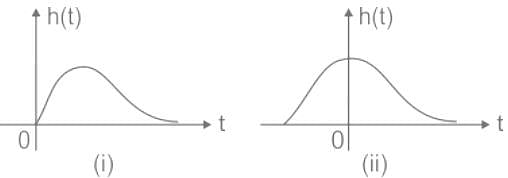
Two systems are shown below, By using 1st system what should be the value of h(t) in the second system?
A stable LTI system has a transfer function 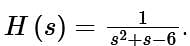 To make this system causal and stable it needs to be cascaded with another LTI system having transfer function H1(s). The correct choice for H1(s) is
To make this system causal and stable it needs to be cascaded with another LTI system having transfer function H1(s). The correct choice for H1(s) is
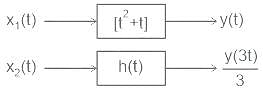
Consider a single input single output discrete-time system with x[n] as input and y[n] as output. Where the two are related as
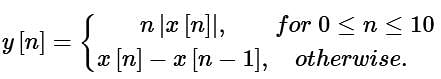
Which one of the following statements is true about the system?
Which of the following statements with respect to the stability of a control system is true?
a. The roots of the characteristic equation are on the left half of the s-plane.
b. The system is bounded input bounded output (BIBO) stable.
c. Stability is independent of the input.
d. The roots of the characteristic equation are on the left half of the s-plane and on the imaginary axis.