All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Tests  >  Test: Hydrostatic Force on Plane Area - 2 - Mechanical Engineering MCQ

Test: Hydrostatic Force on Plane Area - 2 - Mechanical Engineering MCQ


Test Description

10 Questions MCQ Test - Test: Hydrostatic Force on Plane Area - 2

Test: Hydrostatic Force on Plane Area - 2 for Mechanical Engineering 2024 is part of Mechanical Engineering preparation. The Test: Hydrostatic Force on Plane Area - 2 questions and answers have been prepared according to the Mechanical Engineering exam syllabus.The Test: Hydrostatic Force on Plane Area - 2 MCQs are made for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Hydrostatic Force on Plane Area - 2 below.
Solutions of Test: Hydrostatic Force on Plane Area - 2 questions in English are available as part of our course for Mechanical Engineering & Test: Hydrostatic Force on Plane Area - 2 solutions in Hindi for Mechanical Engineering course. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Attempt Test: Hydrostatic Force on Plane Area - 2 | 10 questions in 20 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study for Mechanical Engineering Exam | Download free PDF with solutions
Test: Hydrostatic Force on Plane Area - 2 - Question 1
Save

The greatest and the least depth of a circular plate of 4 m diameter from the free surface of water are 3m and 1 m respectively as shown. What will be the total pressure in (kN) on the plate?

Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 1

Explanation: Total liquid pressure on the lamina = F = γA, where γ = specific weight of the liquid,  = depth of centroid of the lamina from the free surface, A= area of the centroid. Now, γ = 9.81 * 103 N / m3;  = 1 + 3 – 1 / 2 – 2m, A = π ⁄ 4 * 42 = 4π m2. Hence, F = 246.55 kN.

Test: Hydrostatic Force on Plane Area - 2 - Question 2
Save

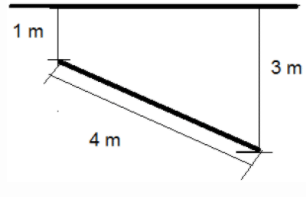
 The greatest and the least depth of a circular plate of 4 m diameter from the free surface of water are 3m and 1 m respectively as shown. What will be the depth (in m) of it’s centre of pressure?

Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 2

Explanation: The depth of the centroid y and the centre of pressure yCP are related by:

where I= the moment of inertia and A = area and θ = the angle of inclination of the lamina to the horizontal. Now,
y = 1 + 3 – 1 / 2 = 2, I = π ⁄ 64 * 42 = 4π, A = π ⁄ 4 * 42 = 4π, sin θ = 1 ⁄ 2 Thus, yCP = 2.125m.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Hydrostatic Force on Plane Area - 2 - Question 3
Save

The highest and lowest vertices of a diagonal of a square lamina (each side equal to 4m) are 1 m and 3 m respectively as shown. What will be the water force (in kN) on the lamina?

Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 3

Explanation: Total liquid pressure on the lamina = F = γA, where γ = specific weight of the liquid,  = depth of centroid of the lamina from the free surface, A= area of the centroid. Now, γ = 9.81 * 103 N / m3;  = 1 + 3 – 1 / 2 = 2m, each side of the lamina =
Hence, F = 156:96 kN.

Test: Hydrostatic Force on Plane Area - 2 - Question 4
Save

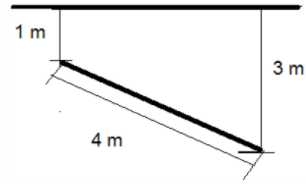
The highest and lowest vertices of a diagonal of a square lamina (each side equal to 4m) are 1 m and 3 m respectively as shown. What will be the depth (in m) of it’s centre of pressure?
Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 4

Explanation:
where I = the moment of inertia and A= area and θ = the angle of inclination of the lamina to the horizontal. Now,  = 1 + 3 – 1 / 2 = 2m, each side of the lamina = =8; sin θ = 3-1/4 = 1 ⁄ 2. Thus, yCP = 2.08m.

Test: Hydrostatic Force on Plane Area - 2 - Question 5
Save

A square lamina (each side equal to 2m) is submerged vertically in water such that the upper edge of the lamina is at a depth of 0.5 m from the water surface. If the pressure on the surface is 12 bar, what will be the total water pressure (in kN) on the lamina?
Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 5

Explanation: Total liquid pressure on the lamina = F = γA, where γ = specific weight of the liquid,  = depth of centroid of the lamina from the free surface, A= area of the centroid. Now, γ = 9.81 * 103 N / m3;A = 2 * 2 = 4 m2. Hence, F = 63.65 kN.

Test: Hydrostatic Force on Plane Area - 2 - Question 6
Save

A container is lled with two liquids of densities ρ1 and ρ2 up to heights h1 and h2respectively. What will be the hydrostatic force (in kN) per unit width of the lower face AB?
Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 6

Explanation: Total liquid pressure on the lamina = F = γA, where γ = specific weight of the liquid,  = depth of centroid of the lamina from the free surface, A= area of the centroid. Now,

Test: Hydrostatic Force on Plane Area - 2 - Question 7
Save

 A container is lled with two liquids of densities ρ and 2ρ up to heights h and eh respectively. What will be the ratio of the total pressure on the lower face AB and on the upper face BC?
Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 7

Explanation: Total liquid pressure on the lamina = F = γA, where γ = specific weight of the liquid,  = depth of centroid of the lamina from the free surface, A= area of the centroid.

Test: Hydrostatic Force on Plane Area - 2 - Question 8
Save

A container is lled with two liquids of densities ρ and 2ρ up to heights h and eh respectively. What will be the ratio of the depths of the centres of pressure of the upper face BC and the lower face AB?
Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 8

Explanation:

Test: Hydrostatic Force on Plane Area - 2 - Question 9
Save

A gate of length 5 m is hinged at A as shown to support a water column of height 2.5 m. What should be the minimum mass per unit width of the gate to keep it closed?
Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 9

Explanation: To keep the gate closed, moment due to weight of the gate should be balanced by the moment due to the hydrostatic force.

where m = mass of the plate, θ = angle of inclination to the horizontal, Fhyd = hydrostatic force on
the plate,   = distance of the point of action of Fhyd from the hinge point = 2⁄3 * 5 = 10⁄3

Fhyd = γA, where γ = specific weight of the liquid = 9.81 * 103  = depth of the centre of pressure from the free surface = 2.5/2 = 1.25 and A = 5 * 1. Substituting all the values in the equation, we get m = 9622.5g.

Test: Hydrostatic Force on Plane Area - 2 - Question 10
Save

A large tank is lled with three liquids of densities ρ1, ρ2 and ρ3 up to heights of h1, h2 and h3 respectively. What will be the expression for the instantaneous velocity of discharge through a small opening at the base of the tank? (assume that the diameter of the opening is negligible compared to the height of the liquid column)
Detailed Solution for Test: Hydrostatic Force on Plane Area - 2 - Question 10

 

Explanation: Instantaneous velocity of discharge  where h= height of the liquid column.

Information about Test: Hydrostatic Force on Plane Area - 2 Page
In this test you can find the Exam questions for Test: Hydrostatic Force on Plane Area - 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Hydrostatic Force on Plane Area - 2, EduRev gives you an ample number of Online tests for practice

Top Courses for Mechanical Engineering

Download as PDF

Top Courses for Mechanical Engineering

Important Questions for Hydrostatic Force on Plane Area - 2

Find all the important questions for Hydrostatic Force on Plane Area - 2 at EduRev.Get fully prepared for Hydrostatic Force on Plane Area - 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Hydrostatic Force on Plane Area - 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Hydrostatic Force on Plane Area - 2 resources.

Hydrostatic Force on Plane Area - 2 MCQs with Answers

Prepare for the Hydrostatic Force on Plane Area - 2 within the Mechanical Engineering exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Hydrostatic Force on Plane Area - 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Hydrostatic Force on Plane Area - 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup