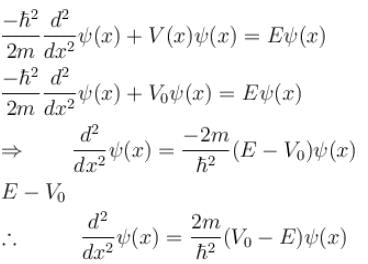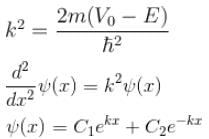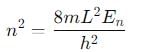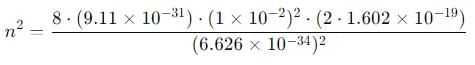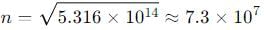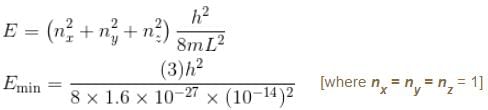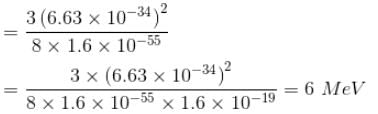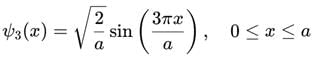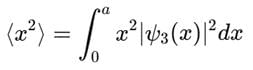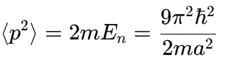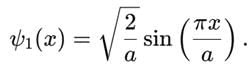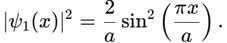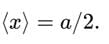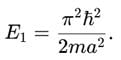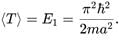Application Of Schrodinger Equation MCQ - Physics MCQ
10 Questions MCQ Test - Application Of Schrodinger Equation MCQ
Probability of finding a particle between 0 to 0.5L in a one-dimensional box of length L in the second excited state is :
Which of the following can be a wave function?
The solution to the Schrodinger equation for a particle bound in a one-dimensional, infinitely potential well, indexed by a quantum number n, indicates that in the middle of the well, the probability density vanishes for.
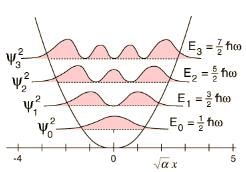
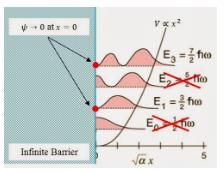
For a particle of mass m, being acted upon by a force with potential energy function 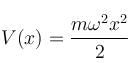 a one-dimensional simple harmonic oscillator. If there is a wall at x = 0 so that V = ∞ for x < 0, then the energy levels are equal to :
a one-dimensional simple harmonic oscillator. If there is a wall at x = 0 so that V = ∞ for x < 0, then the energy levels are equal to :
For a quantum wave particle, E = _____________
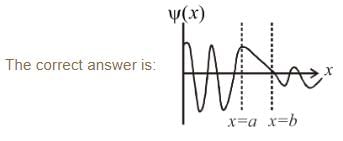
Consider the potential of the form
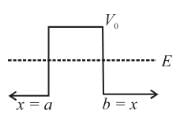
V(x) = 0 for x < a
= V0 for a < x b
= 0 for x > b
Which of the following wave functions is possible for a particle incident from the left with energy E < V0
An electron is trapped in an infinite well of width 1cm. For what value of n will the electron have an energy of 2eV?
If the nucleus is seen as a cubical box of length 10–14 m, then compute the minimum energy of a nucleon confined to the nucleus. Mass of nucleon = 1.6 × 10–27 kg
A particle is in the second excited state (n=3) of a one-dimensional infinite potential well of width a. Which of the following is correct for the expectation values of x, x2, and p2?
A particle is in the ground state of a one-dimensional infinite potential well with boundaries at x=0 and x=a. Which of the following statements is correct?


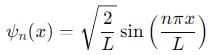
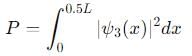
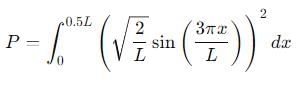
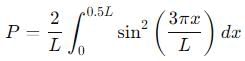
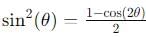 , the integral becomes:
, the integral becomes: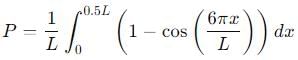
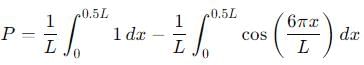
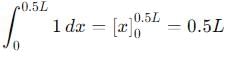
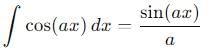

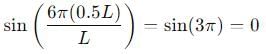
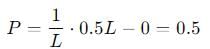



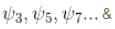 vanishes for
vanishes for 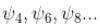 in the middle of the well.
in the middle of the well.