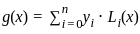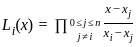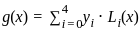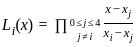CSIR NET Mathematical Science Mock Test - 1 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 1
A seller sells a laptop to Seema at the rate of Rs. 38,804 earning a 9% profit. He sells 2 mobile phones to Arjun, each at the rate of Rs. 13,875 earning a profit of 11% each. What is the total profit he earned on selling a laptop and 2 phones?
If 90 people are to be seated randomly in 15 rows of 6 seats each, what is the probability that a person gets a seat at either end of a row?
The diagrams show the distribution of trees in two forest patches A and B. Each patch is divided into smaller “quadrats”. The number of trees in each quadrat is shown. Which one of the following statements about the means (μ) and standard deviations (σ) of the numbers of trees in the two patches is true?
Forest Patch A

Forest Patch B



A group of 540 persons is to be seated row wise such that the number of persons in each row is 4 less than in the previous row. Which of the following number of rows is not possible?
Among finches males and females have one of the three colours — Red, Blue or Yellow — on their head. During the mating season, males and females pair up randomly. For a large population of finches with 50% red, 30% blue and 20% yellow coloured individuals among both males and females, what is the expected number of pairings between red males and yellow females if the total number of pairs formed is 10000?
The difference of the squares of two distinct two-digit numbers with one being obtained by reversing the digits of the other is always divisible by
Consider two 24-hour clocks A and B. Clock A gets faster by 8 min and clock B gets slower by 12 min every hour. They are synchronised to the correct time at 05 ∶ 00 hrs. Within the following 24 hours at a certain instant clock A shows 15 ∶ 12 hrs and clock B shows 12 ∶ 12 hrs. What is the true time at that instant?
The value of λ for which the integral equation 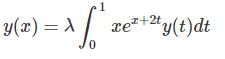 has a non-zero solution, is
has a non-zero solution, is
Let U be an open subset of ℂ and f ∶ U → ℂ be an analytic function. Then which of the following is true?
The critical point of the system 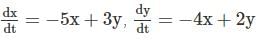 is an
is an
A proportion p of a large population is allergic to peanuts. From this population, a random sample of m people is selected and they all eat a food containing peanuts. At least one of the m people has a subsequent allergic reaction. What is the probability that exactly two of the m people had an allergic reaction?"
Let X be a random variable with cumulative distribution function given by 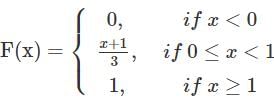 Then the value of
Then the value of 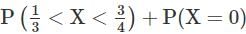
Consider the initial value problem (IVP)
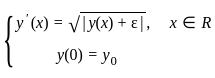
Consider the following statements:
S1: There is an ε > 0 such that for all y0 ∈ ℝ, the IVP has more than one solution.
S2: There is a y0 ∈ ℝ such that for all ε > 0, the IVP has more than one solution.
Then
If u = (x, t) is the solution of the initial value problem
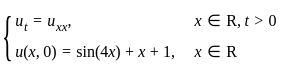
satisfying |u(x. t)| < 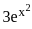 for all x ∈ ℝ and t > 0, then
for all x ∈ ℝ and t > 0, then
Let 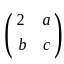 be a 2 x 2 real matrix for which 6 is an eigenvalue. Which of the following statements is necessarily true?
be a 2 x 2 real matrix for which 6 is an eigenvalue. Which of the following statements is necessarily true?
Let C be the positively oriented circle in the complex plane of radius 3 centered at the origin. What is the value of the integral
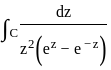 ?
?
Let f(z) = exp , z ∈ ℂ\{0}. The residue of f at z = 0 is
, z ∈ ℂ\{0}. The residue of f at z = 0 is
Let p be a prime number. Let G be a group such that for each g ∈ G there exists an n ∈ ℕ such that gpn = 1. Which of the following statements is FALSE?
Which of the given sequences (an) satisfy the following identity?
A cumulative hazard function G(s) of a non-negative continuous random variable adheres to which of the following conditions?
Consider an integer m ≥ 3. You are given a homogeneous Markov chain on a finite state space {1, 2, …, m} with transition probability matrix Q and initial distribution π. Let Im represent the identity matrix of order m and Tm represent the number of time periods before the chain returns to state 'm' starting from 'm'. Also, assume that the Markov chain is irreducible, but not necessarily aperiodic or ergodic. Which of the following statements are necessarily correct?
Which of the following statements is/are correct?
Define a function f ∶ ℝ → ℝ by
f(x)= 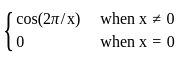
On which of the following subset of ℝ, the restriction of f is a continuous function?
If 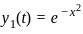 is a solution of differential equation xy" + αy' + βx3y = 0 for some real number α & β then αβ is
is a solution of differential equation xy" + αy' + βx3y = 0 for some real number α & β then αβ is
Which of the following conditions ensure that the power series 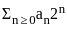 defines an entire function?
defines an entire function?
Let R and S be non-zero commutative rings with multiplicative identities 1R 1S, respectively. Let f: R → S be a ring homomorphism with f(1R) = 1S. Which of the following statements are true?
Let f : ℝ2 → ℝ3 be a differentiable function such that (Df)(0, 0) has rank 2 Writhe f = (f1, f2, f3). Which of the following statements are necessarily true?
The infimum of the set {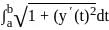 : y ∈ C1[a, b], y(a) = a2, y(b) = b − 5} is
: y ∈ C1[a, b], y(a) = a2, y(b) = b − 5} is
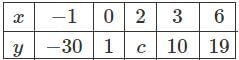
Let g(x) be the polynomial of degree at most 4 that interpolates the data

If g(4) = 5, then which of the following statements are true?



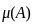 :
: =
= 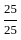 = 1
= 1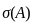 :
: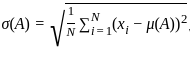
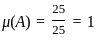 .
. .
.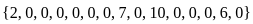
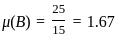 .
. .
.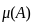 and
and 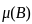 are not equal.
are not equal.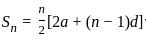
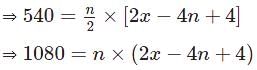
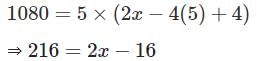


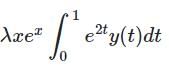
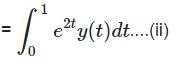
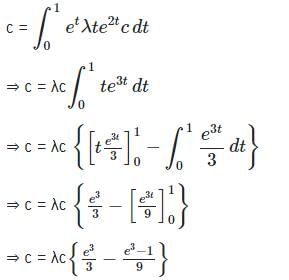
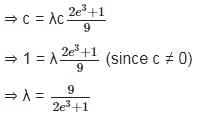
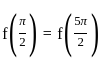
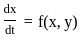
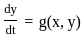

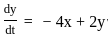
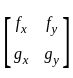 =
= 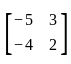

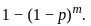
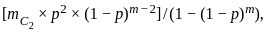 which corresponds to Option A.
which corresponds to Option A.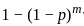 , derives from the property of the binomial distribution where the probability of "at least one success" can be computed as 1 minus the probability of "no success".
, derives from the property of the binomial distribution where the probability of "at least one success" can be computed as 1 minus the probability of "no success".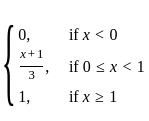
 b) = F(b) - F(a)
b) = F(b) - F(a)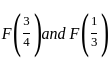 .
.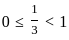 and
and 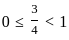 , we use the formula
, we use the formula 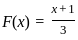 for both 1/3 and 3/4 :
for both 1/3 and 3/4 :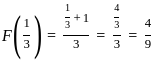
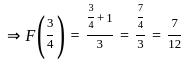
 is:
is: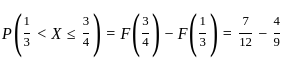
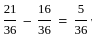
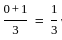
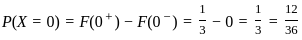
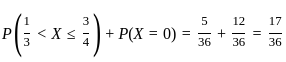
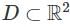 if there exists a constant L > 0 such that for any (x, y1) and (x, y
if there exists a constant L > 0 such that for any (x, y1) and (x, y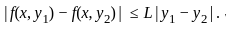
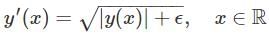
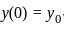 , where ∈ > 0 is a constant, and
, where ∈ > 0 is a constant, and 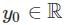 .
.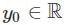 , the IVP has more than one solution.
, the IVP has more than one solution. such that for all ∈ > 0 , the IVP has more than one solution.
such that for all ∈ > 0 , the IVP has more than one solution.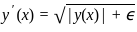 . Since ∈ > 0 , the right-hand side of the equation is always positive and well-defined for any
. Since ∈ > 0 , the right-hand side of the equation is always positive and well-defined for any 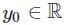 .
.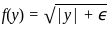 , we need to check if the function satisfies the Lipschitz condition with respect to y.
, we need to check if the function satisfies the Lipschitz condition with respect to y.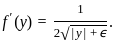
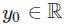 because ∈ > 0 ensures no singularity at y = 0.
because ∈ > 0 ensures no singularity at y = 0.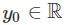 when ∈ > 0 .
when ∈ > 0 .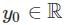 .
.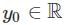 .
.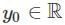 and for all ∈ > 0, the IVP has more than one solution.
and for all ∈ > 0, the IVP has more than one solution.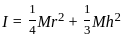
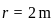 , Height of the cylinder,
, Height of the cylinder, 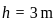 , Density of the cylinder,
, Density of the cylinder, 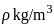
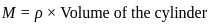 , where
, where 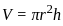
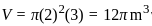
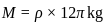
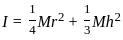
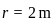 ,
,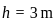 and
and 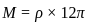 into the formula
into the formula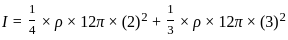
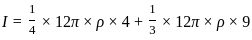
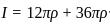
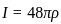
 with the initial condition
with the initial condition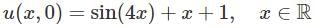 and the solution satisfying the condition
and the solution satisfying the condition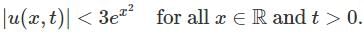
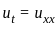 is the classic heat equation. The solution to the heat equation generally smooths out initial conditions over time, but the symmetry of the initial conditions is preserved.
is the classic heat equation. The solution to the heat equation generally smooths out initial conditions over time, but the symmetry of the initial conditions is preserved.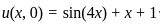 .
.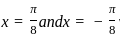
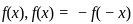 .
.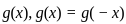 .
.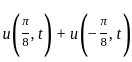 will cancel the odd part and double the even part
will cancel the odd part and double the even part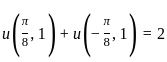
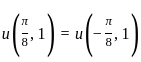
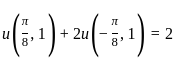

 matrix A is obtained by calculating the determinant of
matrix A is obtained by calculating the determinant of 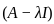 .
.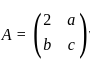 , the characteristic equation is
, the characteristic equation is 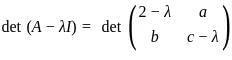
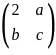 It is stated that 6 is an eigenvalue of this matrix. To determine which of the statements is necessarily true, we will compute the characteristic equation of the matrix and relate it to the given eigenvalue.
It is stated that 6 is an eigenvalue of this matrix. To determine which of the statements is necessarily true, we will compute the characteristic equation of the matrix and relate it to the given eigenvalue.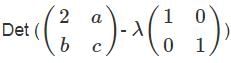
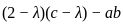
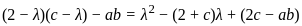
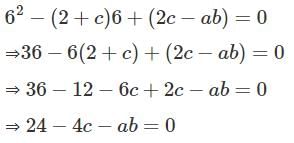
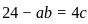
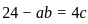
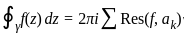
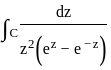 is given by
is given by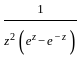 =
= 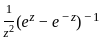
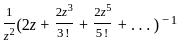 (Expansion of e
(Expansion of e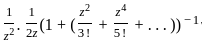
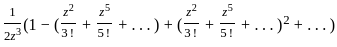 (expansion of (1 + x)-1)
(expansion of (1 + x)-1) = coefficient of 1/z =
= coefficient of 1/z = 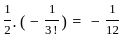
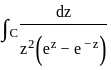 = 2πi(sum of residues) =
= 2πi(sum of residues) = 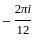 =
= 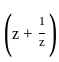
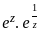


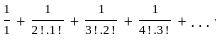
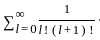
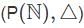 and p = 2 then center of G is infinite.
and p = 2 then center of G is infinite.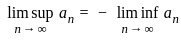
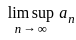 = 0 and
= 0 and 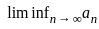 = 0
= 0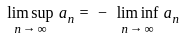 holds
holds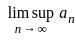 = 1 and
= 1 and 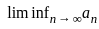 = - 1
= - 1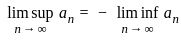 holds
holds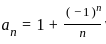 for all n
for all n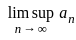 = 1 and
= 1 and 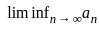 = 1
= 1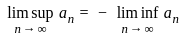 does not hold
does not hold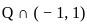
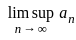 = 1 and
= 1 and  = -1
= -1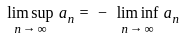 holds
holds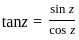
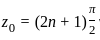
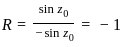
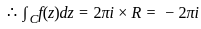
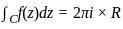
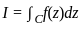 ]
]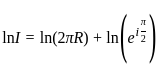
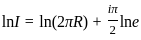
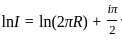
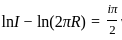

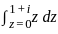
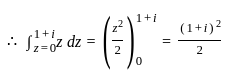

 = f(a)
= f(a)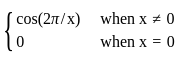
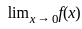 =
= 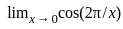 does not exist
does not exist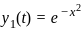 ,
, 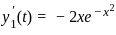 ,
, 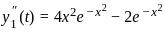
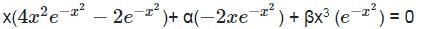
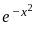
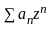 to define an entire function, it must converge for every z
to define an entire function, it must converge for every z 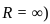 for it to converge everywhere in C .
for it to converge everywhere in C .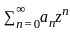 where the coefficients an are such that the radius of convergence R is finite.
where the coefficients an are such that the radius of convergence R is finite.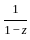 , which converges for |z| < 1.
, which converges for |z| < 1.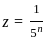 , the value of z decreases as n increases.
, the value of z decreases as n increases.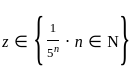 .
.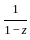 converges. However, for other values of z, such
converges. However, for other values of z, such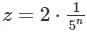 for higher n, the convergence behavior might change depending on the coefficients and radius of convergence.
for higher n, the convergence behavior might change depending on the coefficients and radius of convergence.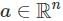 is invertible (i.e., its determinant is non-zero), then there exists an open neighborhood U of a and an open neighborhood V of f(a) such that f : U → V is a diffeomorphism, meaning that f is bijective, and both f and its inverse f-1 are continuously differentiable.
is invertible (i.e., its determinant is non-zero), then there exists an open neighborhood U of a and an open neighborhood V of f(a) such that f : U → V is a diffeomorphism, meaning that f is bijective, and both f and its inverse f-1 are continuously differentiable.