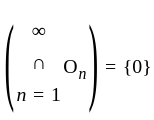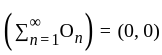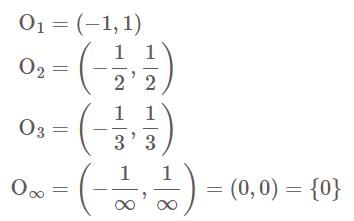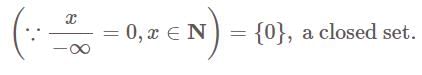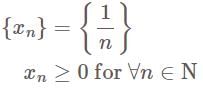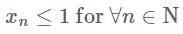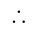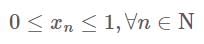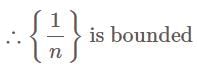CSIR NET Mathematical Science Mock Test - 10 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 10
The mean of six numbers 5, 9, x – 3, x – 1, 16 and 19, is 11. The value of x is:
A solid cannot change its shape easily compared to liquid because of :-
Southern Part of Indian Eastern Coastal Plain is called:
Equal masses of two liquids of densities 3 kg/m3 and 4 kg/m3 are mixed thoroughly. The density of the mixture is-
Two trains of lengths 200 m and 300 m pass each other with constant speeds on parallel tracks in opposite directions. The drivers and guards are at the extremities of the trains. The time gap between the drivers passing each other and first driver-guard pair passing each other is 30s. How much later will the other driver-guard pair pass by?
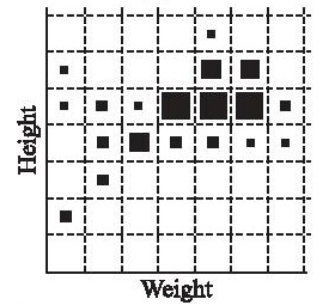
The distribution of heights and weights in a population is shown above in a 2-parameter scatter plot. The size of the square is proportional to the number of persons having a particular combination of weight and height.
Which statement best describes the trend in the population ?
Let p(x) = αx2 + βx + γ be a polynomial where α, β, γ ∈ R. Fix X0 ∈ R.
Let 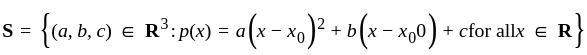
Then the number of elements in S is
The number of 4 digit numbers with no two digit common, is
Let v be the set of all bounded solutions of the 
A farce 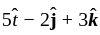 acts on a particle with position vector
acts on a particle with position vector 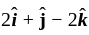 . The torque of the farce about the origin is. (December)
. The torque of the farce about the origin is. (December)
If row vectors of a square matrix A are linearly dependent, then—
The solution of the Cauchy problem for the first order PDE
 on
on 

with the initial condition x2 + y2 = 1, z = 1 is—
 can be transformed to
can be transformed to  for
for 
Let A be a 4 × 4 invertible real matrix. Which of the following is not necessarily true?
Let 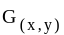 be the Green's function of the boundary value problem
be the Green's function of the boundary value problem 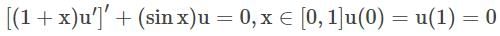 Then the function g defined by
Then the function g defined by
Given a differential equation
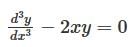
= 0 with initial conditions
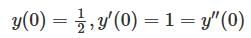
The integral equation is—
If A = {0, 1, 2, 3}, B = {1, -1} and R is a relation from A to B such that (x, y) : x ∈ A, y ∈ B and and y = ix where i is the imaginary number} then the range of R is/an:
An open set that is not an interval is given by
The domain of convergence of the series 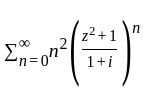 is
is
Given sequence {1/n} —
(A) The nth term is 1/n
(B) The sequence is bounded below
(C) The sequence is bounded above
(D) The sequence is a bounded sequence
Find the correct option:
(A) The set of rational numbers is Lebesgue measurable
(B) The set of rational numbers have Lebesgue outer measure equal to zero
(C) The set of rational numbers is not Lebesgue measurable
(D) The set of rational numbers have Lebesgue out measure equal to one
Let B be an open subset of C and ∂B denote the boundary of B. Which of the following statements are correct ?


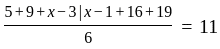
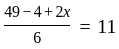
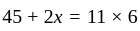
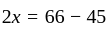
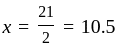

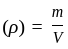
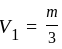
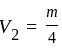
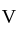
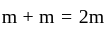
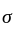
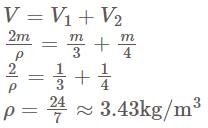

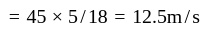
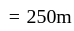
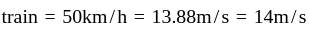
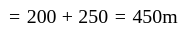
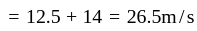
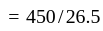
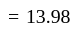 second ~ 14s
second ~ 14s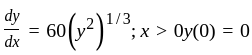 has
has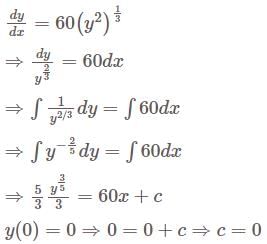
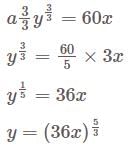
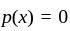 is zero polynomial
is zero polynomial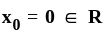
 for
for 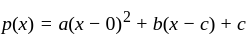
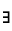 unique
unique 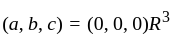
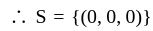
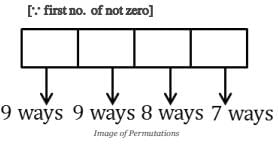
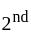 Digit can be choose in = 9 ways
Digit can be choose in = 9 ways Digit can be choose in = 8 ways
Digit can be choose in = 8 ways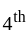 Digit can be choose in = 7 ways
Digit can be choose in = 7 ways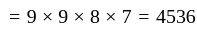
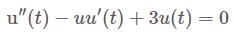
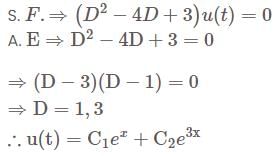

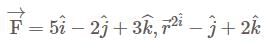
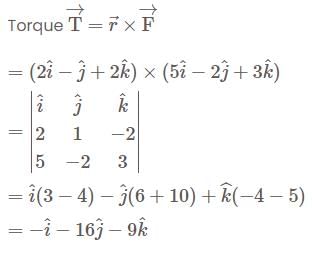
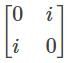 is a-
is a-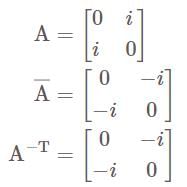
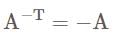
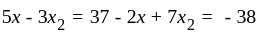 is-
is-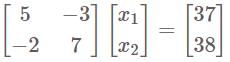
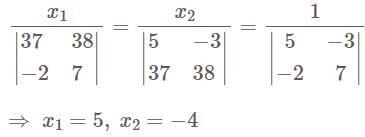
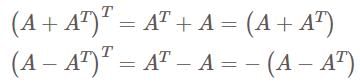


 is unbounded sequence
is unbounded sequence
 is increasing sequence
is increasing sequence  is increasing and unbounded
is increasing and unbounded is divergent
is divergent
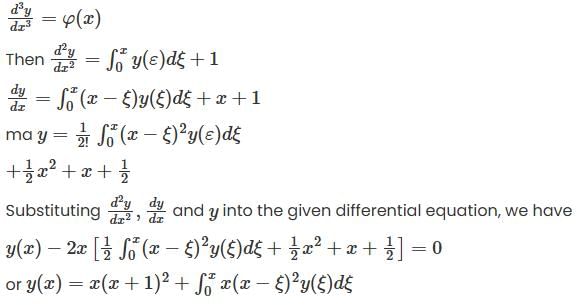
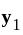 and
and 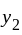 are
are  solution of
solution of 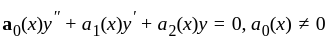 s. t.
s. t.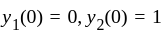
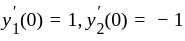
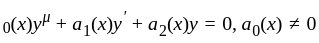

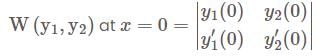
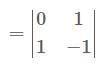
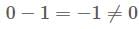
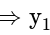 and
and 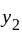 are L. I.
are L. I.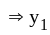 and
and  has no common zeros and
has no common zeros and 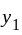 and
and 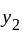 has no common point of extrema
has no common point of extrema (A) and (B) are not true
(A) and (B) are not true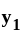 or
or 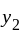 has repeated root
has repeated root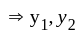 are
are 
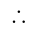 If
If  are
are 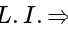 Neither
Neither 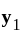 nor
nor 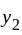 has repeated root
has repeated root and R is a relation from A to B such that
and R is a relation from A to B such that  and
and  where i is the imaginary number}
where i is the imaginary number}
 then
then 
 then
then 
 then
then 

 .
.
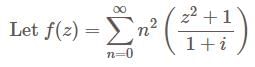
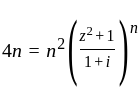
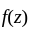 is converges for
is converges for 
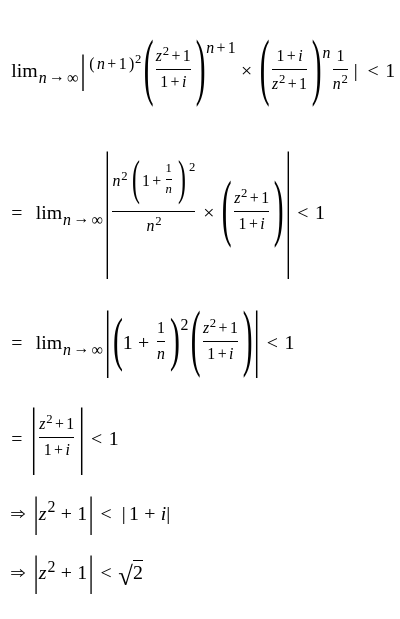
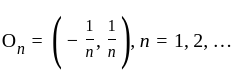
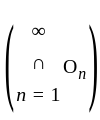 is closed set
is closed set