CSIR NET Mathematical Science Mock Test - 4 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 4
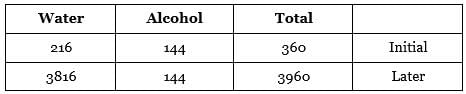
A 360 ml aqueous solution contains 40% alcohol. How much will be the approximate percentage of alcohol if 3600 ml of water is added to the solution?
On a track of 200 m length, S runs from the starting point and R starts 20 m ahead of S at the same time. Both reach the end of the track at the same time. S runs at a uniform speed of 10 m/s. If R also runs at a uniform speed, then how much more time would R take to run the entire course?
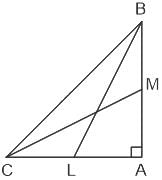
Consider a right angled triangle BAC with medians CM and BL having the same length. The ratio of the length of BC to that of ML is

In a district, every second teacher who teaches chemistry also teaches physics and every third teacher who teaches physics also teaches chemistry. The ratio of teachers who only teach chemistry to those who only teach physics is
An experiment consists of tossing four fair coins independently. The outcome of the experiment is considered favourable, if the number of heads is greater than the number of tails. The probability of a favourable outcome from a single experiment is
On a one-way road, to demarcate 4 lanes, line segments of 3.5 m length are painted with gaps of 3.5 m along the length of the road. What is the total length of the painted lines (in m) over a 350 m stretch of the road?
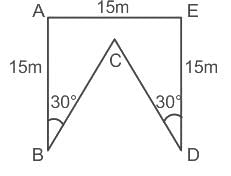
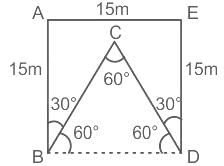
The figure shows map of a field bounded by ABCDE. If AB and DE are perpendicular to AE, then the perimeter of the field is
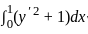 , y(0) = 1, y(1) = 2 is given by
, y(0) = 1, y(1) = 2 is given by
Let u(x, t) be a function that satisfies the PDE
Uxx - Utt = ex + 2t, x ∈ ℝ, t > 0 and the initial conditions
u(x, 0) = cos(x), Ut(x, 0) = 0 for every x ∈ ℝ. Here subscripts denote partial derivatives corresponding to the variables indicated. Then the value of u (π/2, π/2) is
Let C be the collection of all sets S such that the power set of S is countably infinite. Which of the following statements is true?
The number of group homomorphisms from ℤ/150ℤ to ℤ/90ℤ is
Consider the set A = {x ∈ ℚ : 0 < (√2 - 1)x < √2 + 1} as a subset of ℝ. Which of the following statements is true?
Let A1, A2, A3 be events satisfying 0 < P(Ai) < 1 for i = 1, 2, 3. Which of the following statements is true?
Let u = u(x, t) be the solution of the following initial value problem
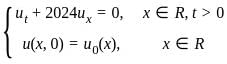
where u0 : ℝ → ℝ s an arbitrary C1 function. Consider the following statements:
S1 : If At = {x ∈ ℝ : u(x, t) < 1} and |At| denotes the Lebesgue measure of A, for every t ≥ 0, then |At| = |A0|, ∀t > 0
S2 : If u0 is Lebesgue integrable, then for every t > 0, the function x → u(x, t) is Lebesgue integrable.
For a quadratic form f(x, y, z) ∈ ℝ[x, y z], we say that (a, b, c) ∈ ℝ3 is a zero of f if f(a, b, c) = 0. Which of the following quadratic forms has at least one zero different from (0, 0, 0)?
Let X1, X2, X3 and X4 he independent and identically distributed Bernoulli (1/3) random variables. Let X(1), X(2), X(3) and X(4) denote the corresponding order statistics. Which of the following is true?
For the unknown y : [0, 1] → ℝ, consider the following two-point boundary value problem: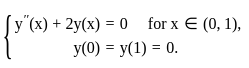 .
.
It is given that the above boundary value problem corresponds to the following integral equation:
y(x) = 2 K(x, t) y(t) dt for x ∈ [0, 1].
K(x, t) y(t) dt for x ∈ [0, 1].
Which of the following is the kernel K(x, t)?
Let x = (x1, …, xn) and y = (y1, …, yn) denote vectors in ℝn for a fixed n ≥ 2. Which of the following defines an inner product on ℝn?
Consider the linear programming problem maximize x + 3y, subject to A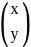 ≤ b, where A =
≤ b, where A = 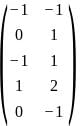 and b =
and b = 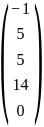 .
.
Which of the following statements is true?
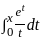 then which of the following is the value of y'(1)
then which of the following is the value of y'(1)
Let E and F be two events in a discrete probability space. Assume that ℙ(E) > 0, ℙ(F) > 0 and that E and F are independent. Which of the following statements are necessarily true?
Consider two independent random variables U and V. U follows a normal distribution with mean 0 and standard deviation 1. V follows a Bernoulli distribution with p = 0.5. Define W as W = U + V.
Which of the following assertions are correct?
Consider the following assertions:
S1: ecos(t) ≠ e2022sin(t) for all t ∈ (0, π).
S2: For each x > 0, there exists a t ∈ (0, x) such that x = loge (1 + xet).
S3: e|sin (x)| ≤ e|x| for all x ∈ ( -1, 1).
Which of the above assertions are correct?
Let f(x) is a function defined as:-
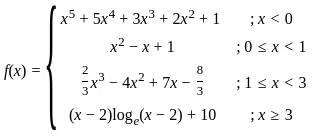
Which of the following statement is/are correct?
The integral equation 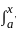 k(x, y) ϕ (y) dy = f(x) with K(x, x) ≠ 0; f or all x can be transformed to ϕ(x) +
k(x, y) ϕ (y) dy = f(x) with K(x, x) ≠ 0; f or all x can be transformed to ϕ(x) + 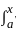 G(x, y) ϕ (y)dy = g(x), where for all x, y
G(x, y) ϕ (y)dy = g(x), where for all x, y
Consider the following ANOVA table for a randomized block design:
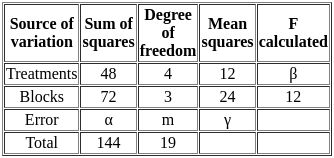
Which of the following statements are true?
Define f : ℝ → ℝ by f(x) = x|x| Which of the following statements are true?


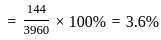
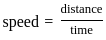

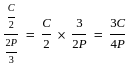
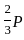 into the equation:
into the equation: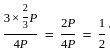
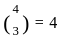 and there is only 1 way to get 4 heads, i.e., HHHH.
and there is only 1 way to get 4 heads, i.e., HHHH.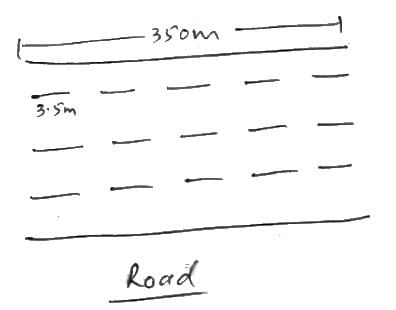
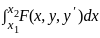 , y(x1) = y1, y(x2) = y2 is give by the Euler equation
, y(x1) = y1, y(x2) = y2 is give by the Euler equation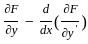 = 0
= 0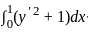 , y(0) = 1, y(1) = 2
, y(0) = 1, y(1) = 2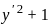 , so using Euler's equation
, so using Euler's equation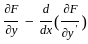 = 0
= 0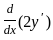 = 0
= 0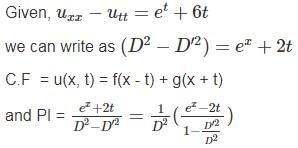
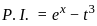
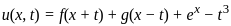
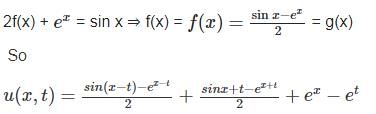
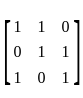
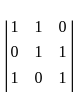 = 1(1 - 0) + 1(1 - 0) = 2 ≠ 0
= 1(1 - 0) + 1(1 - 0) = 2 ≠ 0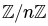 and
and 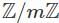 are cyclic groups, the number of group homomorphisms from
are cyclic groups, the number of group homomorphisms from 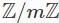 is given by
is given by is given by the greatest common divisor (gcd) of the orders of the two groups. That is Number of homomorphisms = gcd(150, 90)
is given by the greatest common divisor (gcd) of the orders of the two groups. That is Number of homomorphisms = gcd(150, 90)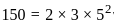
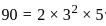
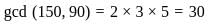
 is 30.
is 30.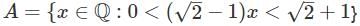 } as a subset of
} as a subset of  , and we need to determine the correct supremum (sup) and infimum (inf) of this set.
, and we need to determine the correct supremum (sup) and infimum (inf) of this set.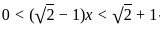 .
.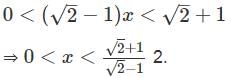
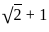
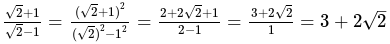
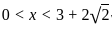
 that satisfy this inequality. Therefore,
that satisfy this inequality. Therefore,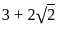 , which is the least upper bound for x.
, which is the least upper bound for x.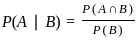 , provided that P(B) > 0.
, provided that P(B) > 0.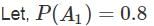
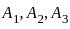 in a probability space with the following probabilities:
in a probability space with the following probabilities: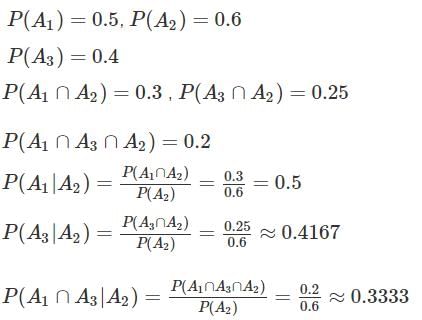

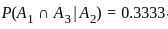


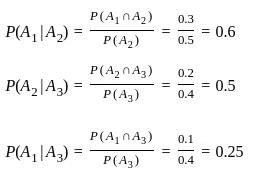

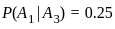
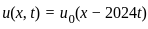 represents a translation of the function
represents a translation of the function 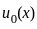 along the x-axis as time t progresses. This is important when analyzing the properties of the solution because many properties, such as integrability and the Lebesgue measure of sets, are preserved under translation.
along the x-axis as time t progresses. This is important when analyzing the properties of the solution because many properties, such as integrability and the Lebesgue measure of sets, are preserved under translation. of a set
of a set 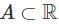 is a way of assigning a "size" to the set.
is a way of assigning a "size" to the set.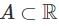 is translated by some fixed amount, its measure remains the same.
is translated by some fixed amount, its measure remains the same.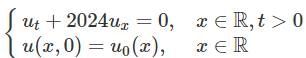
 is an arbitrary C1 (continuously differentiable) function. Two statements S1 and S2 are given about the solution u(x, t), and we are to determine whether both statements are true or false.
is an arbitrary C1 (continuously differentiable) function. Two statements S1 and S2 are given about the solution u(x, t), and we are to determine whether both statements are true or false. has the following characteristic equations
has the following characteristic equations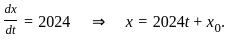
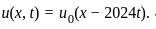
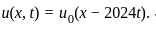
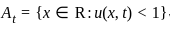 and |At| denotes the Lebesgue measure of
and |At| denotes the Lebesgue measure of 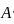 , then for every
, then for every  ,
, 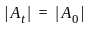 .
.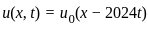 , which means that u(x, t) is a translation of the initial condition.
, which means that u(x, t) is a translation of the initial condition.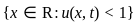 , the measure |At| will remain the same for all t ≥ 0 because the function
, the measure |At| will remain the same for all t ≥ 0 because the function  is simply a translated version of u0(x).
is simply a translated version of u0(x).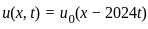 is a translation of the initial condition u0(x).
is a translation of the initial condition u0(x).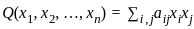 where aij are constants and xi, xj are variables. The zeros of the quadratic form are the values of the variables (x1,x2,…,xn) that make Q(x1,x2,…,xn) = 0
where aij are constants and xi, xj are variables. The zeros of the quadratic form are the values of the variables (x1,x2,…,xn) that make Q(x1,x2,…,xn) = 0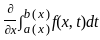 =
= 
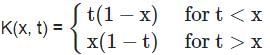
 K(x, t) y(t) dt
K(x, t) y(t) dt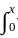 t(1 - x)ydt + 2
t(1 - x)ydt + 2 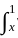 x(1 - t)ydt....(i)
x(1 - t)ydt....(i)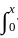 (-t)y(t)dt + x(1 - x)y(x) - 0 + 2
(-t)y(t)dt + x(1 - x)y(x) - 0 + 2 1(1-t)y(t)dt + 0 -x(1 - x)y(x).1
1(1-t)y(t)dt + 0 -x(1 - x)y(x).1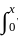
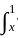
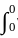
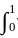

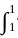
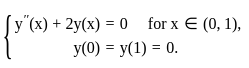 satisfies
satisfies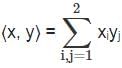 =
= 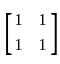
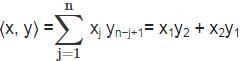
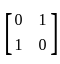
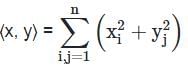
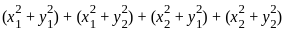
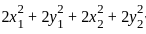
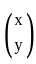 ≤ b,
≤ b,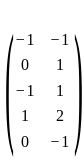 and b =
and b = 
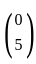
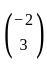
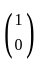 in the feasible region.
in the feasible region.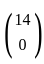
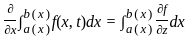 +
+ 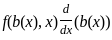 -
- 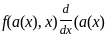
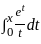
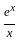 .1 - 0
.1 - 0
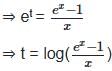
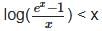
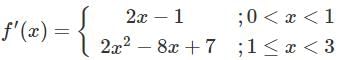
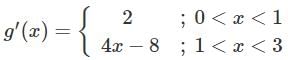
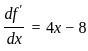
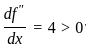
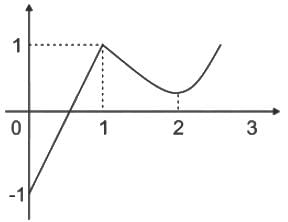
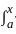 k(x, y) ϕ (y) dy
k(x, y) ϕ (y) dy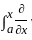 k(x, y)ϕ(y)dy + k(x, x)ϕ(x).1 - 0
k(x, y)ϕ(y)dy + k(x, x)ϕ(x).1 - 0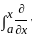
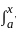 G(x, y) ϕ (y)dy = g(x)....(ii)
G(x, y) ϕ (y)dy = g(x)....(ii)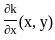
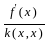 =
= 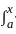
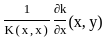
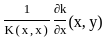
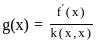
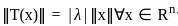 is true only for |λ| = 1
is true only for |λ| = 1
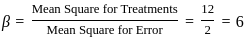
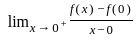
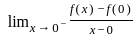
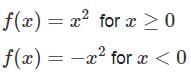
 is true
is true
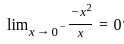 .
.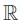 .
.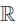 is true
is true










