CSIR NET Mathematical Science Mock Test - 5 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 5
The arithmetic mean of five numbers is zero. The numbers may not be distinct. Which of the following must be true?
Amit Choubey's present age is two third of his mother's age. After ten years the ratio of their ages will be 5 : 7. Find the present ages of both of them in years.
Out of a class of 100 students who can speak at least one of English or Hindi, 41 students can speak English. 21 students can speak both English and Hindi. How many students can speak Hindi?
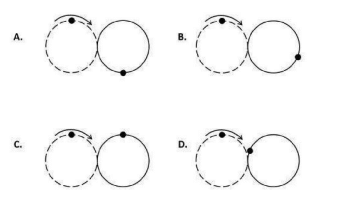
A ting is rolling along a straight track as shown. The topmost point of the ring is marked.

Which of the diagrams shows a possible position of the ring at a later time, relative to the original position (shown by dashed circle)?
A and B have in their collection, coins of Rs. 1, Rs. 2, Rs. 5 and Rs. 10 in the ratio 3 ∶ 2 ∶ 2 ∶ 1 and 4 ∶ 3 ∶ 2 ∶ 1, respectively. The total number of coins with each of them is equal. If the value of coins with A is Rs. 270/-, what is the value of the coins (in Rs) with B?
In an assembly election, parties A, B, C, D and E won 30, 25, 20, 10 and 4 seats, respectively; whereas independents won 9 seats. Based on this data, which of the following statements must be INCORRECT?
A device needs 4 batteries to run. Each battery runs for 2 days. If there are a total of 6 batteries available, what is the maximum number of days for which the device can be run by strategically replacing the batteries till all the batteries are completely drained of power?
In the figure △ABC and △BDC are similar.
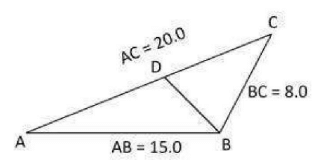
Then BD = ?
The area of one small grid is 9 cm2. What is the perimeter of the shaded region?

Let A =  , a ∈ ℝ. Then for which value of a, A will be positive definite?
, a ∈ ℝ. Then for which value of a, A will be positive definite?
Consider the set of all continuous functions f : [0,1] → [0,1] equipped with the supremum metric. Which of the following statements is true?
Assume that y follows the Poisson distribution with mean λ. If the conditional distribution of X given Y = y is Uniform (0, y) for all y > 0, identify the moment generating function of X (M(t) = E[etX]). Select the correct choice from the following option?
Let 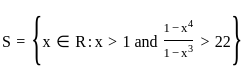 Which of the following is true about S?
Which of the following is true about S?
Consider a petrol pump which has a single petrol dispensing unit. Customers arrive there in accordance with a Poisson process having rate λ = 1 minutes. An arriving customer enters the petrol pump only if there are two or less customers in the petrol pump, otherwise he/she leaves the petrol pump without taking the petrol (at any point of time a maximum of three customers are present in the petrol pump). Successive service times of the petrol dispensing unit are independent exponential random variables having mean 1/2 minutes. Let X denote the average number of customers in the petrol pump in the long run. Then E(X) is equal to
Consider a distribution with probability mass function
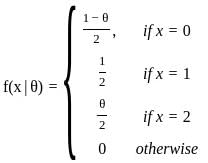
where θ ∈ (0, 1) is an unknown parameter. In a random sample of size 100 from the above distribution, the observed counts of 0,1 and 2 are 20, 30 and 50 respectively. Then, the maximum likelihood estimate of θ based on the observed data is
An analyst considers standardized values of observations on three variables, consumption (C), saving (S) and total income (TI) so that they have zero means and unit variances. She further considers disposable income (DI) where DI =C + S. In the simple linear regressions of DI on TI, DI on C and S on TI, the regression coefficients are 0.8, 0.5 and 0.4, respectively. There are 21 sample observations. Sample covariances and variances are calculated with divisor 20. Then, the value of sum of squared residuals in the regression of DI on S is
The expected number of distinct units in a simple random sample of 3 units drawn with replacement from a population of 100 units is
Let X1....X10 be a random sample from a distribution with the probability density function 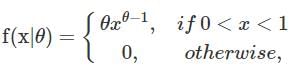
where θ > 0 Is an unknown parameter. The prior distribution of θ is given by
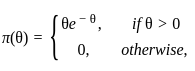
The Bayes estimator of θ under squared error loss is
Let f ∶ ℝ2 → ℝ be a locally Lipschitz function. Consider the initial value problem
ẋ = f(t, x), x(t0) = x0
for (t0, x0) ∈ ℝ2. Suppose that J(t0, x0) represents the maximal interval of existence for the initial value problem. Which of the following statements is true?
Let f(x) = 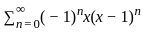 for 0 < x < 2. then which of the following is the value of f(π)
for 0 < x < 2. then which of the following is the value of f(π)
Let Ω be an open connected subset of ℂ containing U = {z ∈ ℂ ∶ |z| ≤ 1/2}.
Let 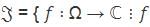 is analytic and supz,w∈U |f(z) − f(w)| = 1}.
is analytic and supz,w∈U |f(z) − f(w)| = 1}.
Consider the following statements:
P: There exists 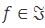 such that |f′ (0)| ≥ 2.
such that |f′ (0)| ≥ 2.
Q: |f(3) (0)| ≤ 48 for all 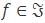 , where f(3) denotes the third derivative of f.
, where f(3) denotes the third derivative of f.
Then
Let T be a M¨obius transformation such that T(0) = α, T(α) = 0 and T(∞) = −α, where α = (−1 + i)/ √2. Let L denote the straight line passing through the origin with slope −1, and let C denote the circle of unit radius centred at the origin. Then, which of the following statements are TRUE?
Consider
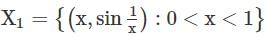
X2 = [0,1] × {0}
X3 = {(0,1)} then
Which of the following statement is/are not true?
Let q1(x1, x2) and q2(y1, y2) be real quadratic forms such that there exist (u1, u2), (v1, v2) ∈ ℝ2 such that q1 (u1, u2) = 1 = q2(v1, v2). Define (x1, x2, y1, y2) = q1 (x1, x2) - q2(y1, y2). Which of the following statements are necessarily true?
Let {Xn}n≥1 be a sequence of independent and identically distributed random variables with E(X1) = 0 and Var(X1) = 1. Which of the following statements are true?


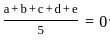
 ).
).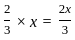 years.
years.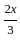 + 10
+ 10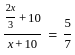
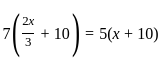
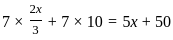
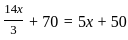
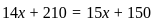
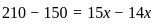

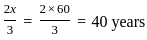

 B| = |A| + |B| - |A
B| = |A| + |B| - |A  B|
B|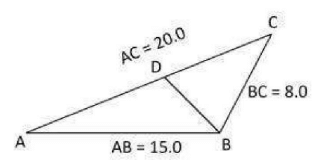
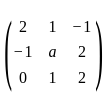 ,
, 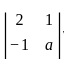 > 0
> 0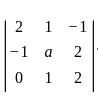 > 0
> 0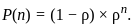
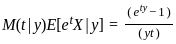
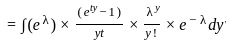
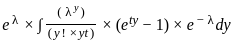
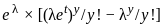 using the property
using the property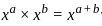
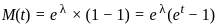
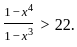
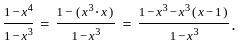
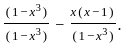
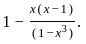
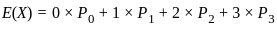
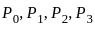 the probabilities for 0, 1, 2, and 3 customers in the system.
the probabilities for 0, 1, 2, and 3 customers in the system.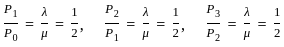
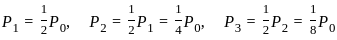
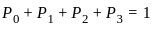
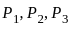 in terms of
in terms of 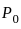 :
: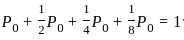
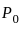 ,
,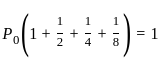
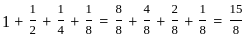
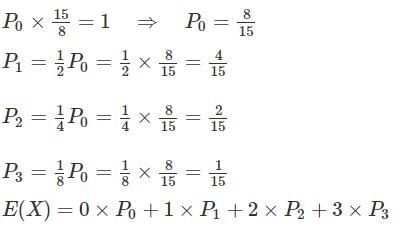
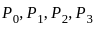 :
: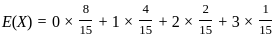
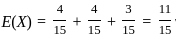
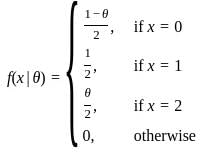
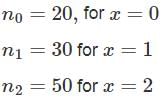
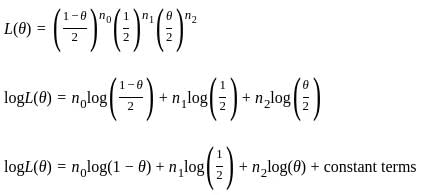
 with respect to θ and set it equal to zero
with respect to θ and set it equal to zero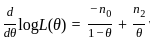
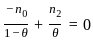
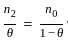
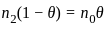
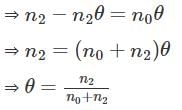
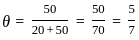
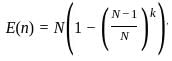
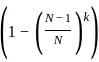 represents the probability that not all selected units are the same, leading to distinct units.
represents the probability that not all selected units are the same, leading to distinct units.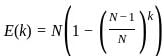
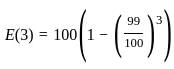
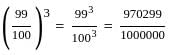
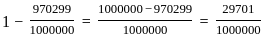
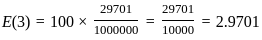
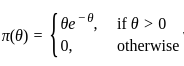
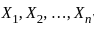 given θ is:
given θ is:
 , the likelihood function is the product of the individual densities
, the likelihood function is the product of the individual densities
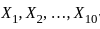 comes from a distribution with the probability density function (pdf):
comes from a distribution with the probability density function (pdf):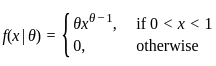 , where θ > 0 is an unknown parameter.
, where θ > 0 is an unknown parameter.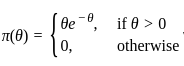
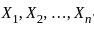 from the given pdf is
from the given pdf is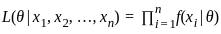
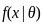 :
: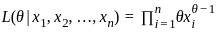
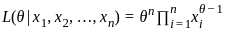
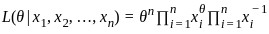
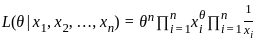
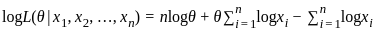
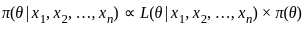
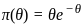 , so
, so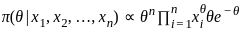
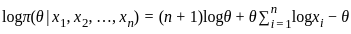
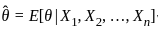
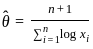

 we put
we put  = 0.
= 0.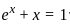
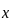 that satisfy this equation. Let’s rewrite this as
that satisfy this equation. Let’s rewrite this as 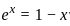

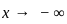 ,
, 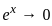 , and
, and 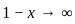 .
.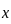 :
: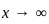 ,
, 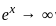 , and
, and 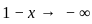 .
.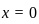 :
: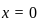 ,
,  , which satisfies the equation.
, which satisfies the equation.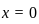 is a solution.
is a solution.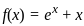 .
.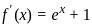
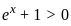 for all real
for all real 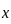 , the function is strictly increasing. Therefore, it can only cross
, the function is strictly increasing. Therefore, it can only cross 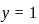 at one point,
at one point,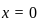 is the only real solution.
is the only real solution.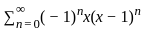
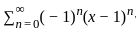
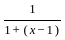
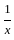
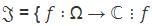 is analytic and
is analytic and 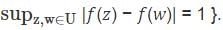
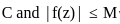 . Let a be a point inside C.
. Let a be a point inside C. 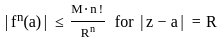
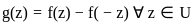
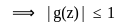
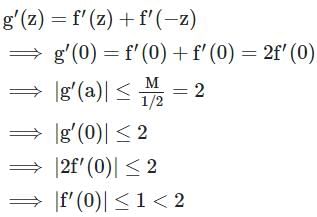
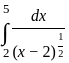
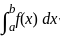 is said to be the improper integral of the first kind if a = -∞ or b = ∞ or both.
is said to be the improper integral of the first kind if a = -∞ or b = ∞ or both.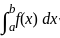 is said to be the improper integral of the second kind if a or b is finite but f(x) is infinite for some x ∈ [a, b].
is said to be the improper integral of the second kind if a or b is finite but f(x) is infinite for some x ∈ [a, b].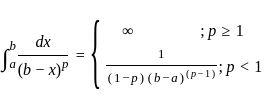 ---(1)
---(1)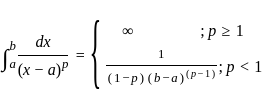 ---(2)
---(2)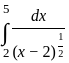
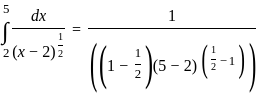
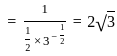
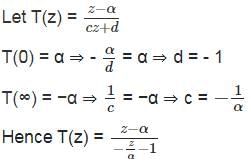
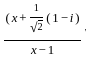
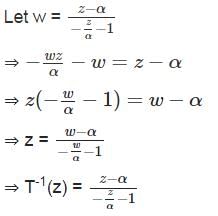
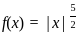
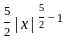 =
= 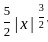
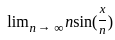
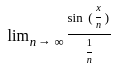
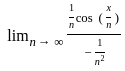
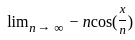 = - ∞
= - ∞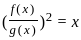
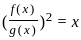 because even degree is never equal to odd degree polynomial.
because even degree is never equal to odd degree polynomial.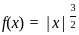 =
= 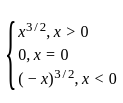
 = 0
= 0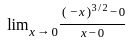
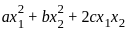 . Quadratic forms are often used to describe curves or surfaces (e.g., ellipses or hyperbolas).
. Quadratic forms are often used to describe curves or surfaces (e.g., ellipses or hyperbolas).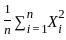 converges to the expected value
converges to the expected value 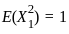 , because X1 has variance 1.
, because X1 has variance 1.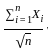 behaves like a standard normal random variable as
behaves like a standard normal random variable as 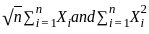 .
.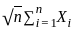 , grows like
, grows like 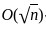 by the Central Limit Theorem since the sum of i.i.d. random
by the Central Limit Theorem since the sum of i.i.d. random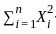 , grows like O(n) because it is the sum of the squares of i.i.d. random variables with variance 1.
, grows like O(n) because it is the sum of the squares of i.i.d. random variables with variance 1.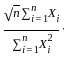 tends to zero, so the probability converges to the probability of the random variable being less than or equal to 0. Hence, Option 1 is true, and the limit will be 1/2 because this becomes a standard normal random variable under large n .
tends to zero, so the probability converges to the probability of the random variable being less than or equal to 0. Hence, Option 1 is true, and the limit will be 1/2 because this becomes a standard normal random variable under large n .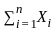 behaves like
behaves like 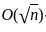 , and the denominator
, and the denominator 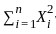 behaves like O(n) . Therefore, the ratio
behaves like O(n) . Therefore, the ratio 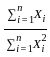 behaves like
behaves like 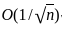 and converges to 0 as
and converges to 0 as 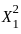 , which is 1, as
, which is 1, as  By the Central Limit Theorem (CLT),
By the Central Limit Theorem (CLT), 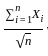 converges in distribution to a standard normal random variable N(0, 1).
converges in distribution to a standard normal random variable N(0, 1).















