CSIR NET Mathematical Science Mock Test - 6 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 6
Mrs. Jain, who was a doctor operating a patient told that the patient is the elder brother of my paternal grandfather's son. What is the relation between the patient and doctor ?
Direction: In each of the following letter series, some of the letters are missing which are given in that order as one of the alternatives below it. Choose the correct alternative.
_ qpp _ pp _ ppq _
What does rise of mercury in a barometer indicate?
Madhvi usually wears a saree, which is 16.66% less than the actual length of the saree. By how much per cent the actual length of the saree is greater than the length of saree which Madhvi usually wears?
The average score of 24 students is 54. If a student’s score was wrongly entered as 64 in place of 88, find the actual average.
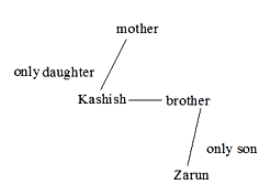
Introducing Zarun, Kashish said, “He is the only son of my mother’s only daughter’s only brother”. How is Kashish related to Zarun?
In a school of 750 boys, the average age of the boys is 15.4 years. The average remains 15.3 if 50 boys leave the school. The average age of the students who left the school-
The average age of a family of 7 members changes from 37 to 31 year due to death of the head of the family. Find the age of the head of the family.
In a single server model, the arrival rate is 5 customer per hour and service rate is 8 customers per hour.
In a group of 3 boys and 2 girls, two children are to be selected such that at least one boy should be there. How many ways are there to do so?
Consider the initial value problem  where
where  is continuous. Then the initial value problem has
is continuous. Then the initial value problem has
The Resolvent kernel 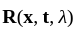 for the volterra integral equation
for the volterra integral equation  is
is
If the matrix B is obtained from the matrix A by interchanging two rows, then—
If matrix A have inverse B and C, then—
Any square matrix A can be expressed as—
The characteristic root for the matrix 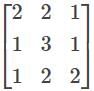 are—
are—
Given the homogeneous integral equation  with degene rate kernel.
with degene rate kernel.
Write {x: x ∈ R, 3 ≤ x ≤ 4} as intervals.
Select the appropiate option:
(A) Every Cauchy sequence is bounded.
(B) Every Cauchy sequence is unbounded
(C) Every Cauchy sequence is convergent
(D) Every Cauchy sequence is divergent
If X is a compact space and L a lattice of continuous real-valued functions on X with the following properties :
(a) L separates points ; that is, if x ≠ y, there is an f ∈ L with f(x) ≠ f(y).
(b) If f ∈ L, and c is any real number, then cf and c + f also belong to L.
Then given any continuous real-valued function h on X and any ∈ > 0.
The collection C of open intervals of the form 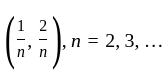 is an open covering of the open interval (0,1)
is an open covering of the open interval (0,1)
If K is a compact metric space and 〈 fn〉 an equicontinuous sequence of functions to a metric space Y that converges at each point of K to a function f
Let A be a complex 3 × 3 matrix with A3 = – 1. Which of the following statements are correct?
A simple random sample of size n is to be drawn from a large population to estimate the population proportion θ. Let p be the sample proportion. Using the normal approximation, determine which of the following sample size values will ensure | p – θ | ≤ 0.02 with probability at least 0.95, irrespective of the true value of θ ? [You may assume Φ(1.96) = 0.975, Φ(1.64) = 0.95, where Φ denotes the cumulative distribution function of the standard normal distribution.]
Let f (x) = ex be approximated by Taylor’s polynomial of degree n at the point x = 1/2 and on the entire interval [0, 1]. If the absolute error in this approximation does not exceed 10–2, then the value of n should be taken as—
Let y be a nonzero vector in an inner product space V. Then which of the following are subspaces of V ?



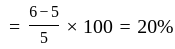
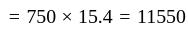
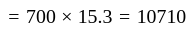
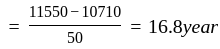
 hour.
hour.



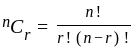
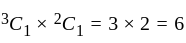









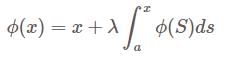
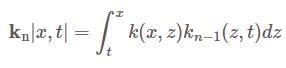
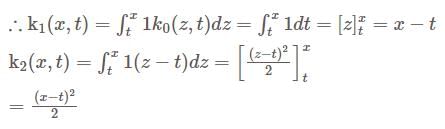
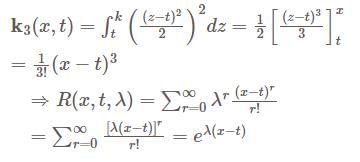
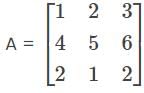 is-
is-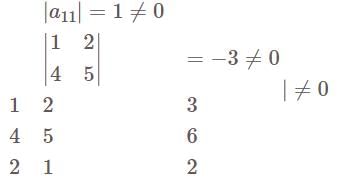


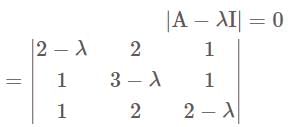
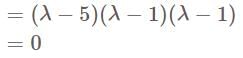

 from
from

 i.e.,
i.e., 

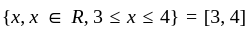
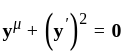 is
is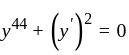
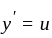
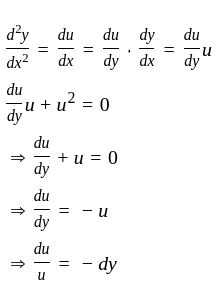
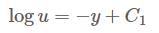
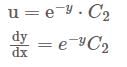
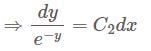
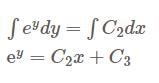
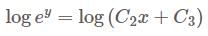

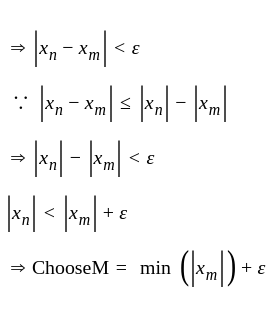
 we have
we have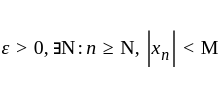
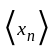 is bounded.
is bounded.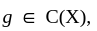 let
let 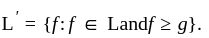 For
For 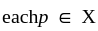 we have
we have  Choose a positive real number
Choose a positive real number 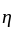 . since
. since 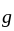 is continuous, the set
is continuous, the set 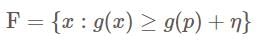 is closed. since
is closed. since 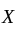 is compact,
is compact, 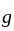 is bounded on
is bounded on 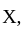 say by
say by 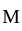 have a function
have a function 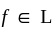 such that
such that 
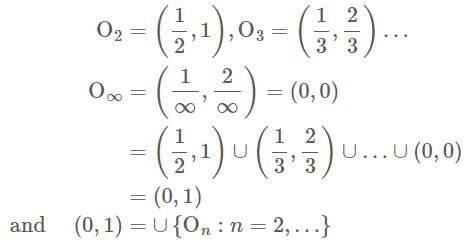

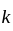
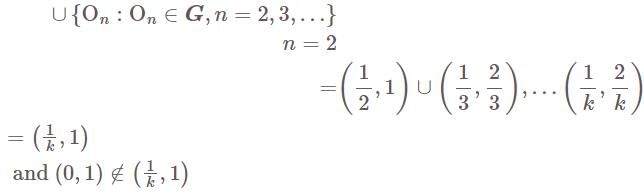
 = −I. Then A3 = −1 but A does not have distinct eigenvalues.
= −I. Then A3 = −1 but A does not have distinct eigenvalues.















