CSIR NET Mathematical Science Mock Test - 8 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 8
A person bought an article and sold it at a loss of 10%. If he had bought for 20% less and sold it for Rs.55 more, he would have had a profit of 40%. Then what is the cost price of the article?
Which of the following steps are required to design a questionnaire?
1. Writing primary and secondary aims of the study.
2. Review of the current literature.
3. Prepare a draft of questionnaire.
4. Revision of the draft.
Select the correct answer from the codes given below:
Which of the following is not a type of Research?
Directions: What will come in place of the question mark (?) in the following number series?
8, 27, 141, 996, ?
Directions: What will come in place of the question mark (?) in the following number series?
6, 42, 163, 419, ?
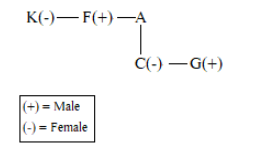
F is the brother of A. C is the daughter of A. K is the sister of F, G is the brother of C. who is the uncle of G ?
Pointing to a gentleman, Radhika said, "His only brother is the father of my son’s father." How is the gentleman related to Radhika?
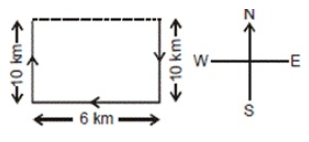
Kalpana drives 10 km towards South, takes a right turn and drives 6 Km. She then takes another right turn, drives 10 km and stops. How far is she from the starting point?
A Shopkeeper keeps the marked price of an item 25% above its cost price. The percentage of discount allowed to gain 10% is-
If ai, bi; and ci are distinct, how many terms will the expansion of the product (a1 + a2 + a3) (b1 + b2 + b3 + b4) (c1 + c2 + c3 + c4 + c5) contain?
The equation of the curve whose sub normal is equal to a constant a is —
Solve the following differential equation:

The number of surjective maps from a set of 4 elements to a set of 3 elements is
What is the Cardinality of the Power set of the set {0, 1, 2}?
The correct polar farm of the complex number 1 - i is:
The area enclosed between the straight line  and the parabola
and the parabola  in the
in the  plane is:
plane is:
If A is a square matrix, then A–1 exist iff—
In a hypothesis-testing problem, which of the following is not required in order to compute the p-value ?
The set of all limit point of the set  is
is
Let  be the vector space of all
be the vector space of all  matrices over
matrices over  . Then the set
. Then the set  , consisting of all matrices which commute with a given matrix
, consisting of all matrices which commute with a given matrix 
i.e. 
If A is open set and B is closed set,
(A) A – B is open set
(B) A – B is closed set
(C) B – A is open set
(D) B – A is closed set
Prove that if f is measurable function and f = g almost everywhere,
Let X1, …, Xn be independent and identically distributed random variables with probability density function—
f(x) = 1/2 λ3x2e–λx; x > 0, λ > 0 Then which of the following statements are true ?
A linear operator T on a complex vector space V has characteristic polynomial x3(x – 5)2 and minimal polynomial x3(x – 5). Choose all correct options—
Let {an}n ≥ 1 be a sequence of positive numbers such that a1 > a2 > a3 > … Then which of the following is/are always true ?


 of
of 

 of
of 








 and
and 
 becomes,
becomes, 






 and
and  then
then















 i
i and
and  .
. ,
,

 is
is
 is bounded
is bounded is
is
 is bounded.
is bounded. is a harmonic function then
is a harmonic function then 


 as independent variable
as independent variable and
and 






 is harmonic function. Then
is harmonic function. Then















 is a subspace
is a subspace




 is a consistent estimator of
is a consistent estimator of 

 we have
we have  naturally isomorphic to
naturally isomorphic to 
 , the induced operator
, the induced operator  on
on  has
has  as its minimal polynomial which implies (4) is false. We can see this by considering the Jordan form of
as its minimal polynomial which implies (4) is false. We can see this by considering the Jordan form of  (It's the lower right
(It's the lower right  submatrix of the above matrix.) Alternatively, let
submatrix of the above matrix.) Alternatively, let 
 Then
Then  If we let
If we let  , then
, then 
 we again have that (4) is false.
we again have that (4) is false.
















