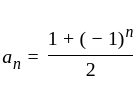Important Questions for CSIR NET Mathematical Science Mock Test - 9
Find all the important questions for CSIR NET Mathematical Science Mock Test - 9 at EduRev.Get fully prepared for CSIR NET Mathematical Science Mock Test - 9 with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the CSIR NET Mathematical Science Mock Test - 9 syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of CSIR NET Mathematical Science Mock Test - 9 resources.
CSIR NET Mathematical Science Mock Test - 9 MCQs with Answers
Prepare for the CSIR NET Mathematical Science Mock Test - 9 within the UGC NET exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for CSIR NET Mathematical Science Mock Test - 9 CSIR NET Exam Mock Test Series 2025
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace CSIR NET Mathematical Science Mock Test - 9 with ease.
Join thousands of successful students who have benefited from our trusted online resources.




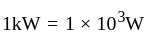
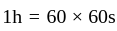
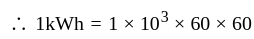
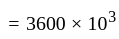
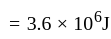
 kilowatt hour is equal to
kilowatt hour is equal to 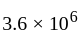 Joule.
Joule.






 gives
gives  ,
, 


 is the inverse of
is the inverse of 


 is
is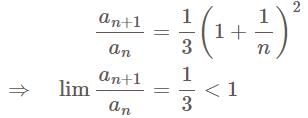
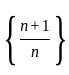 is
is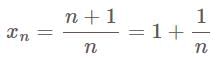
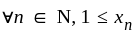 (bounded below)
(bounded below)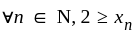 (bounded above)
(bounded above)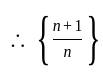 is bounded sequence
is bounded sequence
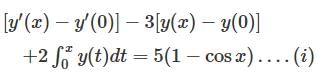
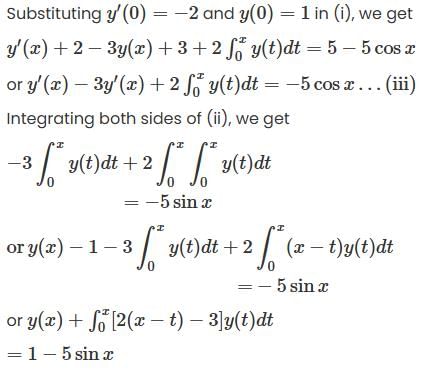
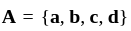 and
and 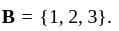 Then which of the following is correct?
Then which of the following is correct?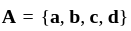 and
and 
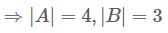
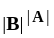
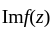 for
for 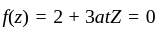 is
is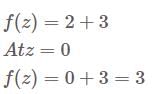
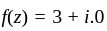
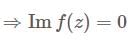
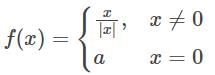

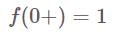
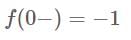
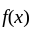 has jump at
has jump at 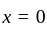
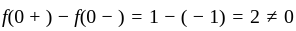
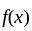 has discontinuity of first kind.
has discontinuity of first kind.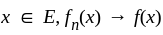 let,
let,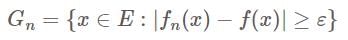
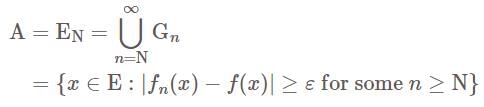
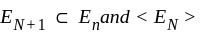 forms a decreasing sequence of measurable sets.
forms a decreasing sequence of measurable sets.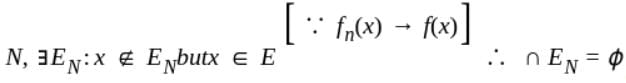 and we have
and we have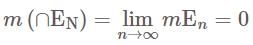
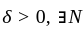 so that
so that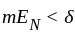 , i.e.
, i.e.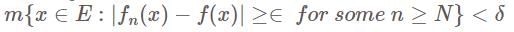
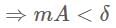
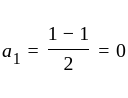
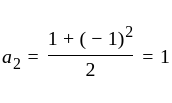
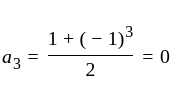
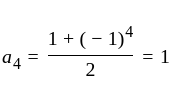
 The
The 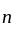 th term of the sequence
th term of the sequence