CSIR NET Mathematics Mock Test - 6 - CSIR NET Mathematics MCQ
30 Questions MCQ Test - CSIR NET Mathematics Mock Test - 6
In which decade was the SPICE simulator introduced?
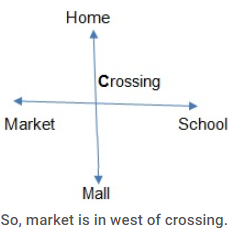
Monica wants to go to the market. She starts from her home which is in the north walk towards south and comes to the crossing. The road to her left ends in a school and straight ahead is a mall and other side is market in which direction is the market to the crossing ?
Direction: In each of the following letter series, some of the letters are missing which are given in that order as one of the alternatives below it. Choose the correct alternative.
_ qpp _ pp _ ppq _
What does rise of mercury in a barometer indicate?
The batting average of a batsman in 57 innings is 58 runs. He was out for a duck in 7 innings. His batting average for remaining innings is -
The average score of 24 students is 54. If a student’s score was wrongly entered as 64 in place of 88, find the actual average.
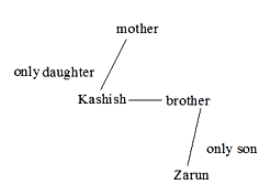
Introducing Zarun, Kashish said, “He is the only son of my mother’s only daughter’s only brother”. How is Kashish related to Zarun?
If  The value of
The value of  for which the vector
for which the vector  belongs to the linear span of
belongs to the linear span of  is
is
The Resolvent kernel 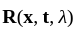 for the volterra integral equation
for the volterra integral equation  is
is
Let A be the matrix of order m × n, then the determinant of A exist if—
Suppose observations on the pair (X, Y) are—
{{}}
Let rp and rs respectively denote the Pearson’s and Spearman’s rank correlation coefficient between X and Y based on the above data. Then which of the following is true?
If f : [0, 1] → (0, 1) is a continuous mapping then which of the following is not true ?
How many normal subgroups does a nonabelian group G of order 21 have other than the identity subgroup {e} and G ?
Let V be a vector space of all 2 x 2 matrices and W be A subset of all matrices having determinant zero, then
Select the appropiate option:
(A) Every Cauchy sequence is bounded.
(B) Every Cauchy sequence is unbounded
(C) Every Cauchy sequence is convergent
(D) Every Cauchy sequence is divergent
Let A and B be two sets of positive real numbers bounded above. Let a = sup A and b = sup B. If C = {xy : x ∈ A and y ∈ B}
If φ and ψ are simple functions which vanish outside a set of finite measure.
Let A be a complex 3 × 3 matrix with A3 = – 1. Which of the following statements are correct?
A simple random sample of size n is to be drawn from a large population to estimate the population proportion θ. Let p be the sample proportion. Using the normal approximation, determine which of the following sample size values will ensure | p – θ | ≤ 0.02 with probability at least 0.95, irrespective of the true value of θ ? [You may assume Φ(1.96) = 0.975, Φ(1.64) = 0.95, where Φ denotes the cumulative distribution function of the standard normal distribution.]



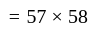
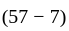 or 50 innings
or 50 innings 


 eq. (1)
eq. (1)
 (3)
(3)

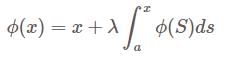
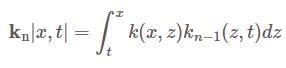
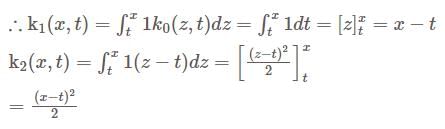
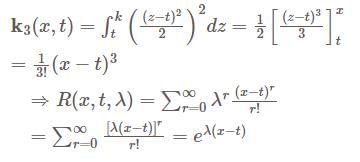
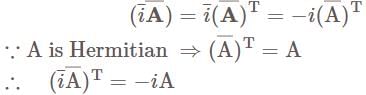

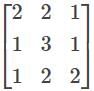 are—
are—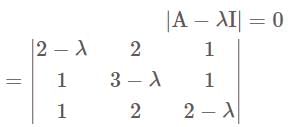
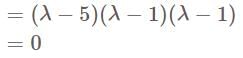
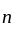 th term
th term 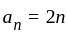
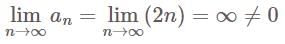
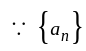 is does not converges to zero
is does not converges to zero 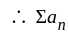 is divergent.
is divergent.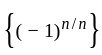 converges to
converges to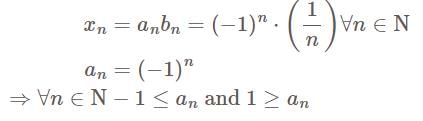
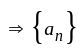 is a bounded sequence
is a bounded sequence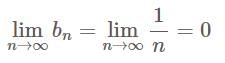
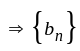 is converges to zero
is converges to zero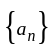 is bounded sequence and
is bounded sequence and 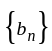 conver ges to zero
conver ges to zero 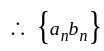 converges to zero.
converges to zero.
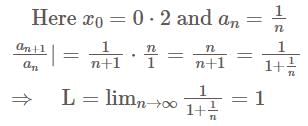
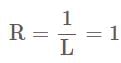
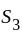 has a cyclic subgroup
has a cyclic subgroup 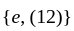 of order 2. It is not normal because
of order 2. It is not normal because 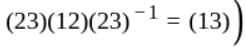
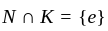
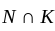 divides 3 and 7, so is 1 ). Their product NK is thus the whole group G, since it has order
divides 3 and 7, so is 1 ). Their product NK is thus the whole group G, since it has order 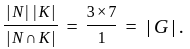 (To see this consider the map
(To see this consider the map 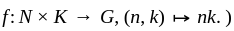 So any
So any 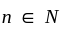 and
and 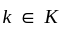 commute. (Consider an element of the form
commute. (Consider an element of the form 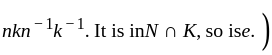
 with
with 








 is
is

 is
is 

 is
is  sin
sin 
 I.
I.






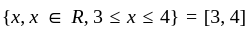
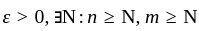
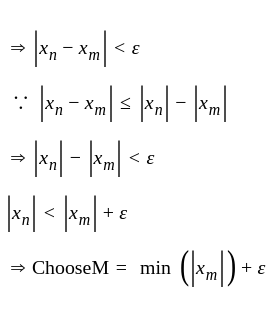
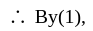 we have
we have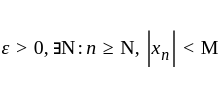
 is bounded.
is bounded.

















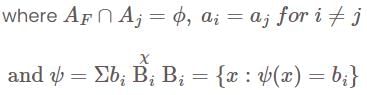
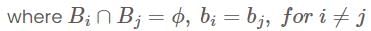
 , then they form a disjoint collection of measurable sets and can be represented as,
, then they form a disjoint collection of measurable sets and can be represented as,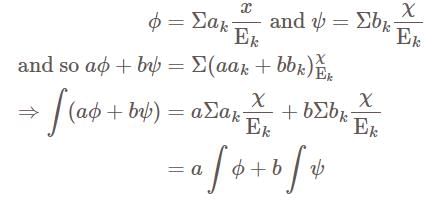
 = −I. Then A3 = −1 but A does not have distinct eigenvalues.
= −I. Then A3 = −1 but A does not have distinct eigenvalues.















