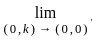CUET PG Mathematics Mock Test - 3 - CUET PG MCQ
30 Questions MCQ Test - CUET PG Mathematics Mock Test - 3
Is the transformation T(x, y, z) = (x, y, 0) linear?
If A and B are 3 × 3 real matrices such that rank (AB) = 1, then rank (BA) cannot be
Match List - I with List - II

Choose the correct answer from the options given below:

Choose the correct answer from the options given below:
For which value of k, the function f(x) = 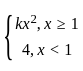 is continuous at x = 1?
is continuous at x = 1?
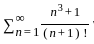 then which of the following is correct?
then which of the following is correct?
If the eigen values of a 3 × 3 matrix are 6, 5 & 2 what is the determinant of (A-1)T.
Consider the sequence (an)_{n ≥ 1}, where an = cos( (-1)^n * (nπ/2) + (nπ/3) ).
Which one of the following statements is true?
Let W be a solution space of the differential equation 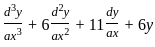 = 0. Then dimension of the solution space W is
= 0. Then dimension of the solution space W is
Which of the following is correct? (where C-R equation means Cauchy Riemann Equation)
The directional derivative of Ø(x, y, z) = x2yz + 4xz2 at (1, -2, 1) in the direction of 2î - ĵ - 2k̂ is
A basic feasible solution of an m × n transportation problem is said to be non-degenerate, if basic feasible solution contains exactly _______ number of individual allocations in ______ positions.
The solution of the differential equation y = px + √(4 + p²) is
If z = exsiny, x = loget and y = t2 then dz/dt is given by the expression
Let f(x) be a polynomial satisfying f(0) = 2, f'(0) = 3 and f''(x) = f(x). Then f(4) is equal to
The system of equations
x + y + z = 150
x + 2y + 3z = 100
2x + 3y + 4z = 200 has
For a given matrix P = 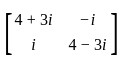 , where i = √-1, the inverse of matrix P is
, where i = √-1, the inverse of matrix P is
Consider the following statements:
I. Every infinite group has infinitely many subgroups.
II. There are only finitely many non-isomorphic groups of a given finite order.
Then
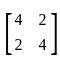 the eigenvalue corresponding to the eigenvector
the eigenvalue corresponding to the eigenvector 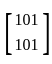 is
is
lim n→∞ ( (1 / (n+1)) + (1 / (n+2)) + ... + (1 / 2n) ) is equal to
Let V and W be the subspaces of R4 defined as
V = {(a, b, c, d) : b - 5c + 2d = 0}, W = {(a, b, c, d) : a - d = 0, b - 3c = 0}, then the dimension of V ∩ W.
Given a square matrix A which of the following will always be true?
(I). AᵀA = AAᵀ
(II). A - Aᵀ is skew symmetric
(III). A⁻¹ exists
(IV). (Aᵀ)⁻¹ = (A⁻¹)ᵀ
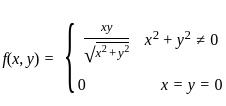 , Then Which of the following is not Correct ?
, Then Which of the following is not Correct ?



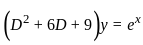
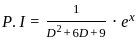
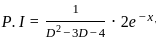
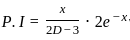
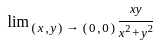 is :
is :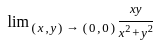
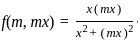
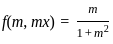
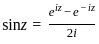
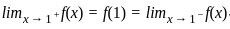
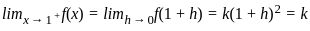
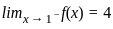
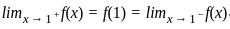
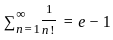 and
and 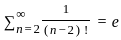
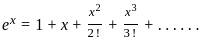
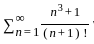
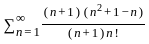
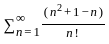
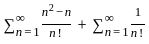
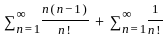
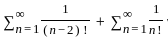
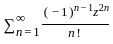 is
is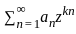 is
is 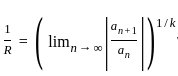
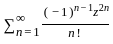 ,
, 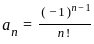 and k = 2
and k = 2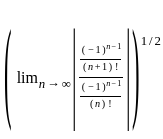
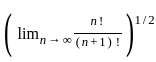
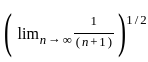
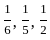 respectively.
respectively.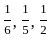 .
.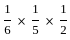
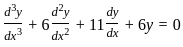
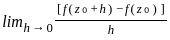
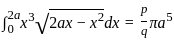 , then p
, then p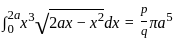
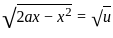
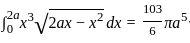

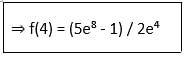
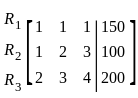
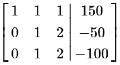

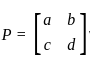 then |P| = (a × d) - (b × c)
then |P| = (a × d) - (b × c)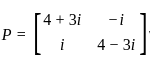
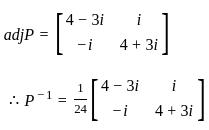
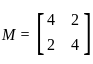
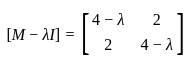
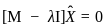
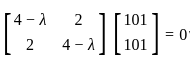
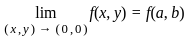
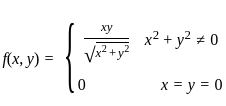
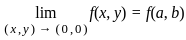 and finite.
and finite.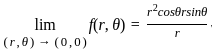 = 0
= 0 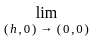 {f(h, 0) - f(0, 0)} / h = 0
{f(h, 0) - f(0, 0)} / h = 0