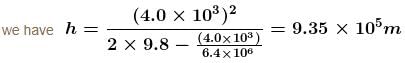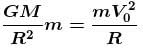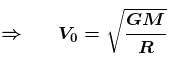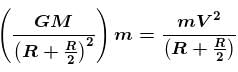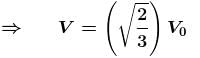Central Forces NAT Level – 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Central Forces NAT Level – 1
The change in the value of g at a height h above the surface of the earth is the same as at a depth d below that surface of earth. When both d and h are much smaller than the radius of earth, then, d = αh. Find the value of α.
Energy required to move a body of mass m from an orbit of radius 2R to 3R is 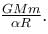 Find the value of α
Find the value of α
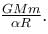 Find the value of α
Find the value of αA satellite in a circular orbit of radius r has time period of 4hrs. A satellite with orbital radius of 4r around the same planet will have a time period of in hours.
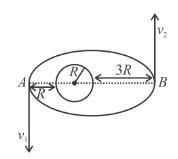
The minimum and maximum distances of a satellite from the centre of earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth. The radius of curvature at the point of minimum distance is λR. Find the value of λ.
Maximum height reached by a rocket fired with a speed equal to 50% of the escape velocity from Earth’s surface is R/α. Find the value of α.
Two satellites S1 and S2 of equal masses revolves in the same sense around a heavy planet in coplanar circular orbit of radii R and 4R. Find the value of 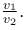
Radius of the earth is R and the means density is ρ. Find out the gravitational potential at the earth’s surface απGρR2. Find the value of α.
A body which is initially at rest at a height R above the surface of the earth of radius R, falls freely towards the earth. Find out its velocity (in m/s) on reaching the surface of earth.
Take g = 10m/s2 and R = 6400km.
A particle is projected from the surface of earth with an initial speed of 4.0km/s. Find the maximum height (in kms) attained by the particle.
The orbital velocity of an artificial satellite in a circular orbit just above the earth’s surface is V0. The value of orbital velocity for another satellite orbiting at an altitude of half of earth’s radius is  Find the value of α.
Find the value of α.


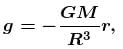 where r is the distance from centre
where r is the distance from centre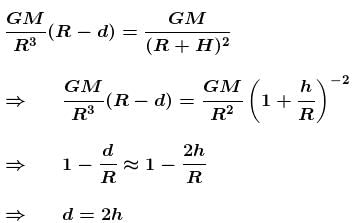
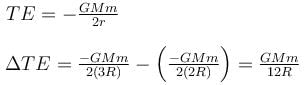

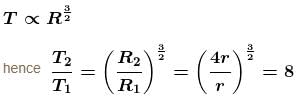
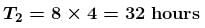
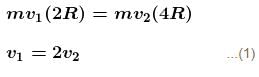
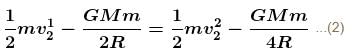


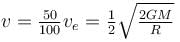
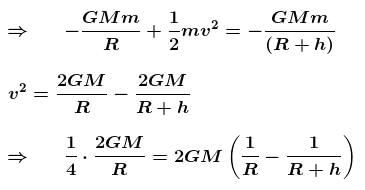
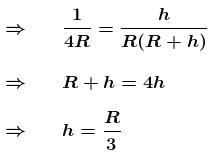
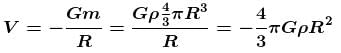
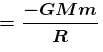
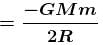
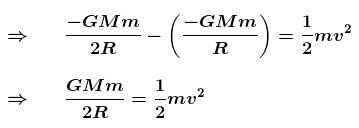
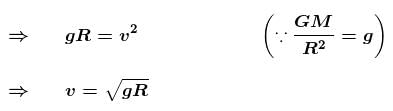
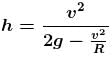 and g = 9.8 m/s2.
and g = 9.8 m/s2.