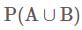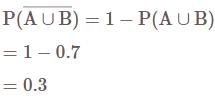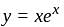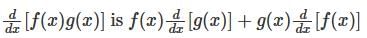DSSSB TGT Mathematics Mock Test - 6 - DSSSB TGT/PGT/PRT MCQ
30 Questions MCQ Test DSSSB TGT Mock Test Series 2025 - DSSSB TGT Mathematics Mock Test - 6
The first Indian to swim across English channel was
Who is the author of the book 'The Future of Freedom'?
The major towns namely Fatehabad, Hissar, Firozpur, Jaunpur and Firozabad were founded by :
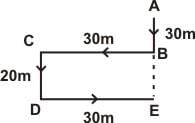
A man walks 30 metres towards South. Then, turning to his right, he walks 30 metres. Then, turning to his left, he walks 20 metres. Again, he turns to his left and walks 30 metres. How far is he from his initial position?
Select the correct figure from the given Answer Figure that would complete the Question figure.

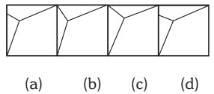
Directions to Solve
In each of the following questions find out the alternative which will replace the question mark.
Question -
3 : 12 :: 5 : ?
Select the option that expresses the given sentence in passive voice.
They will have brought the toy.
Direction: Read the passage carefully and answer the following questions.
We are living in truly challenging times. The loss of near and dear ones in the second surge of the Covid pandemic is painful. Those who have died include not only ordinary people but also eminent doctors, academics, business leaders, literary and public figures, editors and journalists, civil servants, and people from the judicial fraternity. Their grief has to be our grief, too, because only by sharing sorrow can we develop a true national resolve.
Yet, there is a glimmer of hope. The positivity rate is declining, and new cases are down in 200 districts. The rate of recovery is a satisfying 86.7 percent. As on May 19, nearly 18.58 crore doses of vaccine have been administered. There is a well-laid-out plan to increase the production capacity of vaccines. Covaxin production is projected to increase from 1.5 crore doses per month to 10 crore doses by September. Similarly, Covishield is projected to increase its production up to 10 crore doses per month by August. This, along with Sputnik and many other vaccines in the pipeline, implies that the government has a clear roadmap for the production of 216 crore vaccines before the end of this year.
It is necessary to understand the scale of the challenge. In the first wave of Covid, the total number of cases in one year — from March 31, 2020, to March 31, 2021 — as per WHO data, was 1.20 crore approximately. The fatality percentage was 1.34 percent. In contrast, in the second wave, within a short span of 49 days — from April 1 to May 19 — the total number of Covid cases reported was 1.31 crore and the fatality percentage was 1.10 percent. Yet, there is hope in this WHO data. Deaths per lakh population in India was 21, whereas it was 181 in the USA, 166 in France, 195 in the UK, 209 in Italy, 171 in Spain, and 106 in Germany. I must clarify that any death anywhere is very painful.
Q. Which one of the following statements is TRUE according to the passage?
Direction: Change the Narration.
Q. He said, “She has finished her homework“.
निम्न में से अशुद्ध वर्तनी वाला विकल्प चुनिए।
निम्नलिखित पर्यायवाची में से विछोह का पर्यायवाची शब्द बताओ ?
निर्देश: निम्नलिखित गद्यांश को ध्यानपूर्वक पढ़िए व प्रश्नों के उतर दीजिये:
जन्मजात लोकतंत्रवादी वह होता है, जो जन्म से ही अनुशासन का पालन करने वाला हो। लोकतंत्र स्वाभाविक रूप में उसी को प्राप्त होता है, जो साधारण रूप में अपने को मानवीय तथा दैवीय सभी नियमों का स्वेच्छापूर्वक पालन करने का अभ्यस्त बना ले। जो लोग लोकतंत्र के इच्छुक हैं उन्हें चाहिए कि पहले वे लोकतंत्र की इस कसौटी पर अपने को परख लें। इसके अलावा, लोकतंत्रवादी को नि:स्वार्थ भी होना चाहिए। उसे अपनी या अपने दल की दृष्टि से नहीं बल्कि एकमात्र लोकतंत्र की ही दृष्टि से सब-कुछ सोचना चाहिए। तभी वह सविनय अवज्ञा का अधिकारी हो सकता है। व्यक्तिगत स्वतंत्रता की मैं कदर करता हूँ, लेकिन आपको यह हरगिज नहीं भूलना चाहिए कि मनुष्य मूलत: एक सामाजिक प्राणी ही है। सामाजिक प्रगति की आवश्यकताओं के अनुसार अपने व्यक्तित्व को ढालना सीखकर ही वह वर्तमन स्थिति तक पहुँचा है। अबाध व्यक्तिवाद वन्य पशुओं का नियम है। हमें व्यक्तिगत स्वतंत्रता और सामाजिक संयम के बीच समन्वय करना सीखना है। समस्त समाज के हित के खातिर सामाजिक संयम के आगे स्वेच्छापूर्वक सिर झुकाने से व्यक्ति और समाज, जिसका कि वह एक सदस्य है, दोनों का ही कल्याण होता है।
Q. लोकतंत्र में एक लोकतंत्रवादी को कैसा होना चाहिए?
The product of two consecutive positive integers is 360. To find the integers, this can be represented in the form of quadratic equation as:
Find the quadratic equation whose one root is 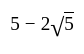 .
.
Let two events 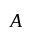 and
and 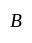 be such that
be such that 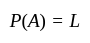 and
and  . Which one of the following is correct?
. Which one of the following is correct?
A man wants to cut three lengths from a single piece of board of length  . The second length is to be
. The second length is to be 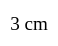 longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least
longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 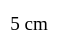 longer than the second?
longer than the second?
In a class, 54 students are good in Hindi only, 63 students are good in Mathematics only and 41 students are good in English only. There are 18 students who are good in both Hindi and Mathematics. 10 students are good in all three subjects.
What is the number of students who are good in Hindi and Mathematics but not in English?
Given that N = {1, 2, 3, …, 100}, then write B, the subset of N whose elements are represented by x + 2, where x is ∈ N.
If the magnitude of the sum of two non-zero vectors is equal to the magnitude of their difference, then which one of the following is correct?
There are 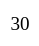 people in a group. If all shake hands with one another, how many handshakes are possible?
people in a group. If all shake hands with one another, how many handshakes are possible?
Consider the following statements:
I. A' ∪ B = (A ∩ B)'
II. (ϕ')' = ∪
III. A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Which of the statement(s) given above is/are correct?
Let 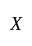 be a non-empty set and let
be a non-empty set and let 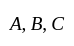 be subsets of
be subsets of 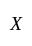 , consider the following statements:
, consider the following statements:
1. 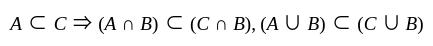
2. 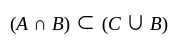 for all sets
for all sets 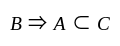
3. 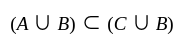 for all sets
for all sets 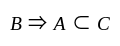
Which of the above statements is/are correct?
There are 2 shirts, 3 jeans, 3 socks and 2 skirts. In how manys ways a shopkeeper can arrange these things so that all the socks come together and all the skirts come together?
If 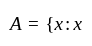 is an isosceles triangle
is an isosceles triangle 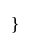 and
and 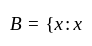 is an equilateral triangle
is an equilateral triangle  then find
then find 
If A and B are two events such that 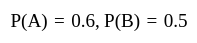 and
and 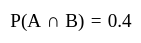 , then consider the following statements:
, then consider the following statements:
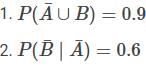
Which of the statements is/are correct?
If x =, y =
, z =
where a, b, c are in AP and |a| < 1, |b| < 1, |c| < 1, then x, y, z are in



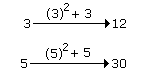

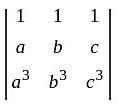 .
.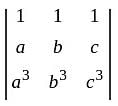
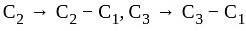 , we get
, we get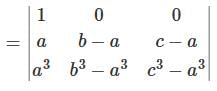
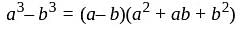
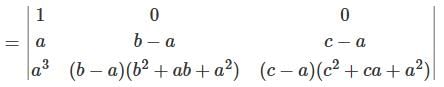
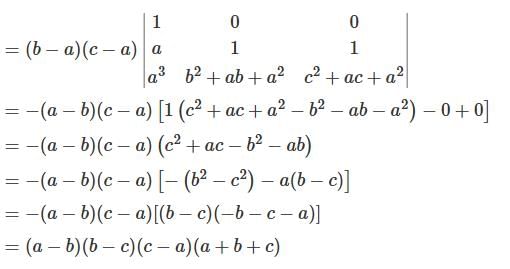
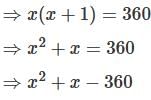
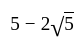
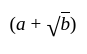 then the other roots must be conjugate
then the other roots must be conjugate 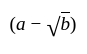 and vice-versa.
and vice-versa.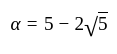 and
and 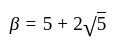
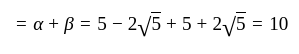
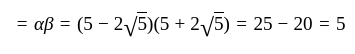
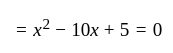
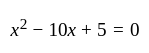 .
.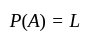 and
and 
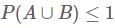 (∵ Max value of probability is 1)
(∵ Max value of probability is 1)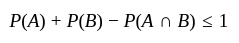
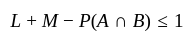

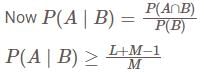
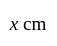 .
. According to the question, length of the second piece
According to the question, length of the second piece 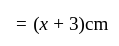 .
.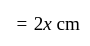 .
. .
.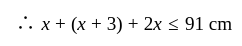
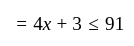
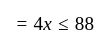
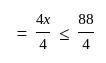
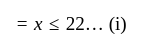
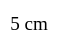 longer than the second piece.
longer than the second piece.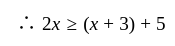
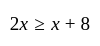
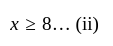
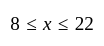
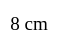 and less than or equal to
and less than or equal to  .
.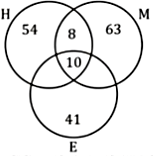
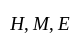 denote the set of students studying Hindi, Mathematics and English.
denote the set of students studying Hindi, Mathematics and English.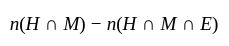
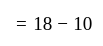
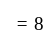
 is equal to:
is equal to: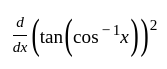 ...(1)
...(1)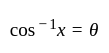 ...(2)
...(2)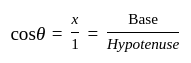
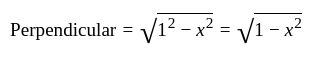
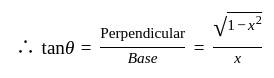
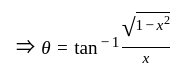
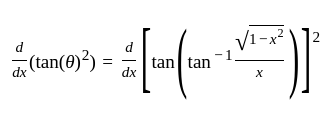
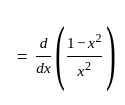
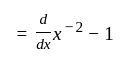
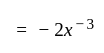
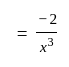
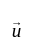 and
and 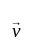 be two non-zero vectors.
be two non-zero vectors.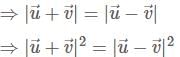
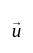 be a vector then
be a vector then 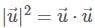
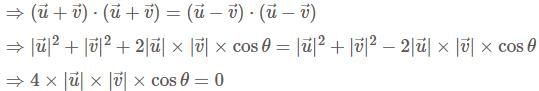
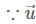 and
and 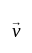 be two non-zero vectors
be two non-zero vectors 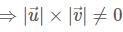
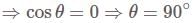
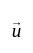 and
and 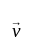 are perpendicular to each other.
are perpendicular to each other. people
people 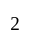 people
people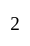 people can be selected out of
people can be selected out of 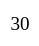 So the answer is
So the answer is 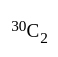
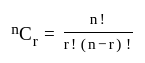
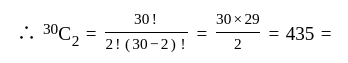 Number of handshakes
Number of handshakes be subsets of
be subsets of 
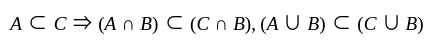
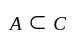 then
then 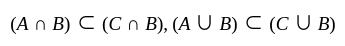 is true.
is true.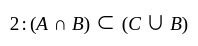 for all sets
for all sets 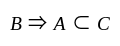
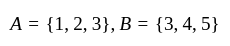 and
and 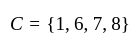
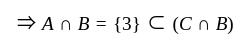 but
but 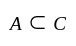 is not true.
is not true.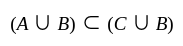 for all sets
for all sets 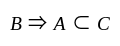
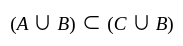 for all sets
for all sets 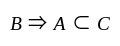
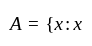 is an isosceles triangle
is an isosceles triangle  and
and 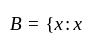 is an equilateral triangle
is an equilateral triangle 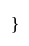
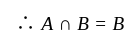
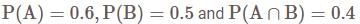
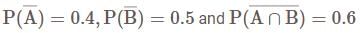
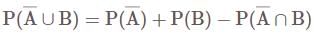
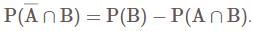
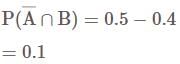
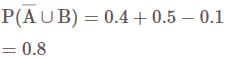
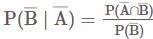
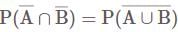 .
.