Differential Equation MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Differential Equation MCQ Level - 2
(D2 - 1)y = x sin x + (1 + x2)ex, will be satisfied by which of the following functions?
If [(x + 1)2 f(x) – g(x)] is the particular integral of the differential equation,
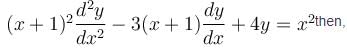
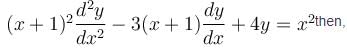
The general solution of the differential equation 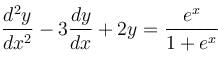 will be :
will be :
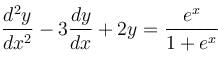 will be :
will be :Given that the differential equation (axy2 + by)dx + (bx2y + ax)dy = 0, (a ≠ b) is not exact. If xmyn is an integrating factor of the given equation, then
The slope of the tangent at the point (x, y) to a curve passing through 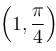 is given by,
is given by, 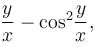 then the equation of the curve is :
then the equation of the curve is :
The general solution of the equation, (D2 - 6D + 8)y = (e2x - 1)2 + sin3x will be :
If (x, y) is the solution to the system of equations,
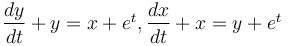
then x is equal to :
The curve orthogonal to the curve x2 + 2xy – y2 = k would be :
The particular integral of the differential equation, 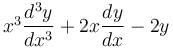 = x2 log x + 3x is
= x2 log x + 3x is
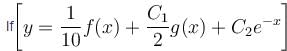 is the solution of the differential equation, D2y + 1 (1 - cot x) Dy - y cot x = sin2 x then
is the solution of the differential equation, D2y + 1 (1 - cot x) Dy - y cot x = sin2 x then


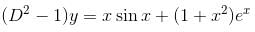 The auxiliary equation is
The auxiliary equation is
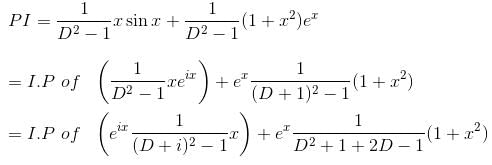
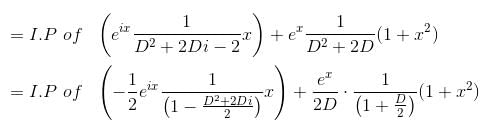
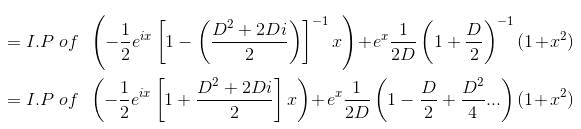
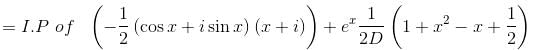
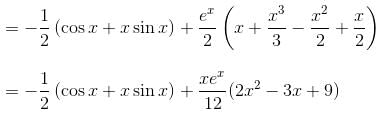
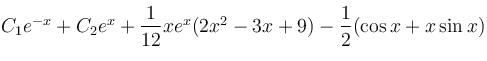
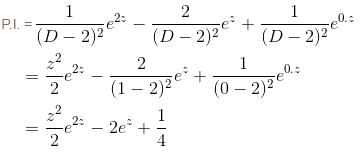
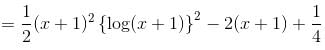
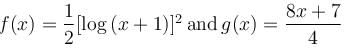

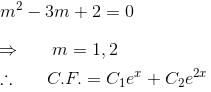
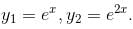 Their wronskian is
Their wronskian is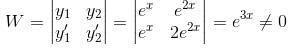
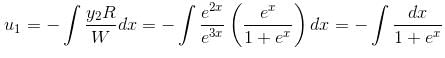
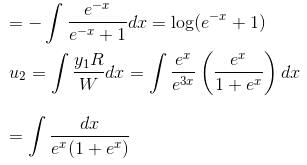
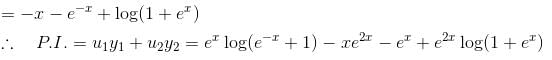
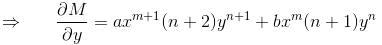
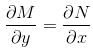
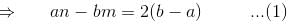
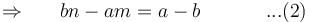
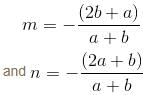
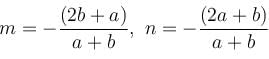
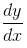
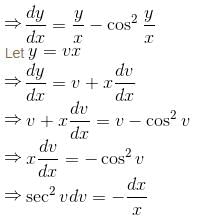
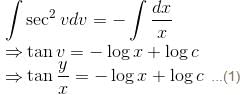
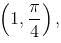 so it will satisfy the equation of the curve.
so it will satisfy the equation of the curve.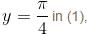
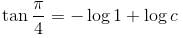
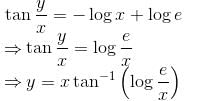
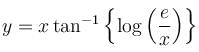
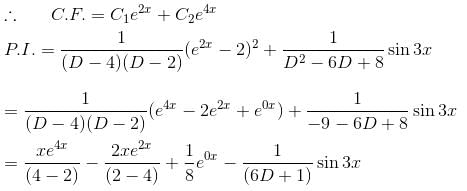
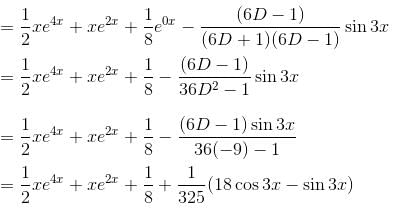
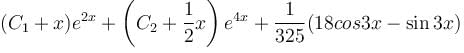
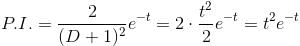
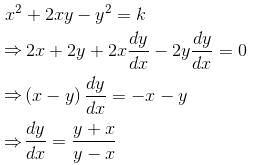
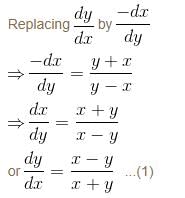
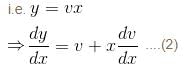
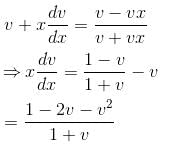
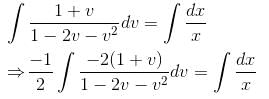
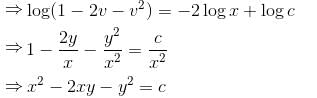
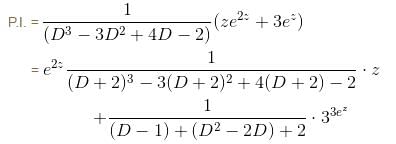
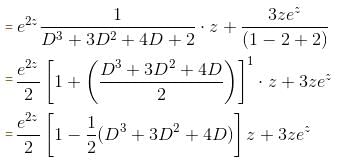
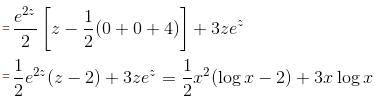
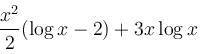
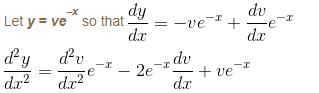
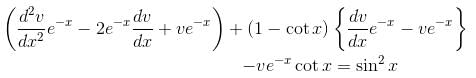
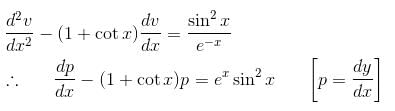
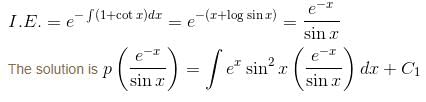
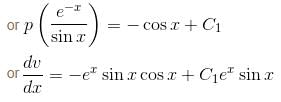
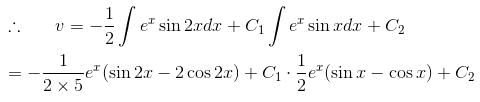

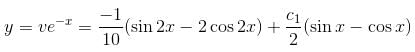 is the required solution.
is the required solution.











