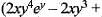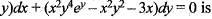Differential Equations - 5 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Differential Equations - 5
The interval for x, over which the solution of IVP dy(2 + x2 + y2) -dx (1 + 2x + 3y) = 0,y(0) = 0, R : |x| ≤ 2, |y| ≤ 1 exists, is
let n be a non-negative integer. The eigen values of the Sturm-Lioville problem 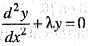 with boundary condition y(0) =
with boundary condition y(0) = 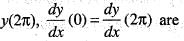
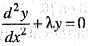 with boundary condition y(0) =
with boundary condition y(0) = 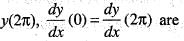
The initial value problem 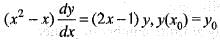 has a unique solution, if (x0, y0) equals
has a unique solution, if (x0, y0) equals
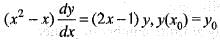 has a unique solution, if (x0, y0) equals
has a unique solution, if (x0, y0) equalsOne of the points which lies on the solution curve of the differential equation (y – x) dx + (x + y) dy = 0, the curve passes through (0,1)
The solution of the differential equation 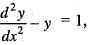 which vanishes when x = 0 and tends to a finite limit as x → -∞ is
which vanishes when x = 0 and tends to a finite limit as x → -∞ is
If u1, u2, u3 are solutions of the equation 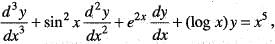 then 2u1 + au2 + bu2 and au1 + bu2 + u3 are also solutions of given differential equation, then the values of a and b are
then 2u1 + au2 + bu2 and au1 + bu2 + u3 are also solutions of given differential equation, then the values of a and b are
The largest value of c such that there exists a function h(x) for -c < x < c that is a solution dy/dx = 1 +y2 with h(0) = 0 is given by
Let y1 and y2 be two linearly independent solutions of y" + (sin x)y = 0, 0 ≤ x ≤ 1
Let g(x) = W(y1, y2) (x) be the Wronskian of y1 and y2.
Then,
If y1(x) and y2(x) are solutions of y" + x2y' - (1 - x) y = 0 such that y1(0) = 0 ,y1'(0 ) = -1 and y2(0) = - 1, y2' (0) = 1, then the Wronskian W(y1, y2) on R
For the sturm-Liouville problem (1 + x2)y" + 2xy' + λx2y = 0 with y'(1) = 0 and y'(10) = 0 the eigen values, λ satisfy
Consider the following statement for IVP 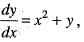 y(0) = 1 ,D : |x| ≤ 1, |y - 1 | ≤ 1
y(0) = 1 ,D : |x| ≤ 1, |y - 1 | ≤ 1
I. It has a solution which exists for all n
II. The local interval for which the solution exists uniquely is 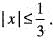
III. It has no solution in the interval |x| ≤ 3.
Then select the correct code.
Let y(x) be a non-trivial solution of the 2nd order linear differential equation
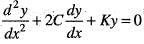
where C < 0; K > 0 and C2 > K, then
Let y1(x) and y2(x) be two linearly independent solution of the differential equation 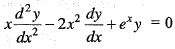 satisfying y1(0) = 1, y2(0) = -1 y'1(0) = 1 and y'2( 0) = 1. Then, the Wronskian of y1(x) and y2(x) at x = 2, i.e.,
satisfying y1(0) = 1, y2(0) = -1 y'1(0) = 1 and y'2( 0) = 1. Then, the Wronskian of y1(x) and y2(x) at x = 2, i.e.,  is equal to
is equal to
The coordinate at a moving point P satisfying the equations 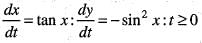 of the curve passes through the point (π/2, 0). When t = 0, then the equation of the curve in rectangular coordinates is
of the curve passes through the point (π/2, 0). When t = 0, then the equation of the curve in rectangular coordinates is
Let y1 and y2 be solutions of Bessel’s equation t2y" + ty' + (t2 - n2)y = 0 on the interval 0 < t < ∝ with y1(1) = 1, y'1 (1) = 0, y2(1) = 0 and y'2(1) = 1, then value of W[y1, y2] (t) is
Let A be a 3 x 4 matrix of rank 2. Then the rank of ATA, where AT denotes the transpose of A. is,
The solution of y" + ay' + by = 0 where a and b are constants, approaches to zero as x → ∝ then
For the initial value problem y' = f(x,y) with y(0) = 0,
which of the following statement is true?
|
27 docs|150 tests
|