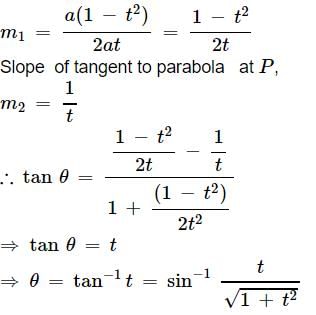EmSAT Mathematics Mock Test-4 - Grade 8 MCQ
30 Questions MCQ Test - EmSAT Mathematics Mock Test-4
Sum and the product of zeroes of the polynomial x2 +7x +10 is
If “1” is a zero of the polynomial P(a) = x2a2 – 2xa + 3x – 2, then x = ______
In an experiment a solution of hydrochloric acid is to be kept between 30 and 35 degree celcius. What is the range of temperature in degree Fahrenheit if conversion formula is given by 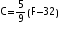 ,where C and F represent temperature in degree celsius and degree fahrenheit, respectively?
,where C and F represent temperature in degree celsius and degree fahrenheit, respectively?
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 5}, B = {6, 7}. Then A ∩ B’ is:
Direction: Read the following text and answer the following questions on the basis of the same:
A Mathematics Exhibition is being conducted in your School and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience.
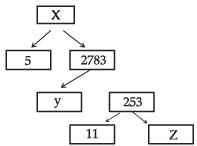
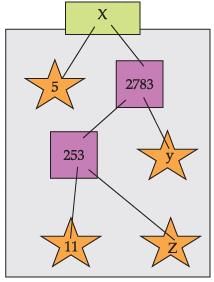
What will be the value of y?
Let z = x + iy be a complex number where x and y are integers then the area of the rectangle whose vertices are the roots of the equation
If | a | = 2, | b | = 5 and | a × b | = 8, thencan be equal to
If A, B are symmetric matrices of same order then the matrix AB-BA is a
A cube is 7 cm on an edge and another cube is 14 cm on an edge. The ratios of their curved surface areas are
A school organised an educational trip to Taj Mahal. Mathematics teacher of the school took her 9th standard students to it. The teacher had interest in history as well. She narrated the facts to Taj Mahal to students. Then the teacher said in this monument one can find combination of solid figures. There are 4 pillars which are cylindrical in shape. The Taj Mahal has a larger white dome surrounded by four smaller domes.

Q. How much cloth material will be required to cover 4 small domes each of radius 2 m?
Direction: Read the following text and answer the below questions:
Seema placed a light bulb at point O on the ceiling and directly below it placed a table. Now, she put a cardboard of shape ABCD between table and lighted bulb. Then a shadow of ABCD is casted on the table as A'B'C'D' (see figure). Quadrilateral A'B'C'D' in an enlargement of ABCD with scale factor 1 : 2, Also, AB = 1.5 cm, BC = 25 cm, CD = 2.4 cm and AD = 2.1 cm; ∠A = 105°, ∠B = 100°, ∠C = 70° and ∠D = 85°.
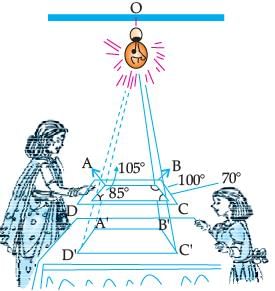
What is the sum of angles C' and D'?
In the given figure perpendiculars are dropped on the common base BD of the given two triangles. AE = 2cm, CF = 3cm
If A + B + C = p & sin = k sin C/2,then tan A/2 tan B/2 =
The equation of a straight line passing through the point (3, 6) and cutting the curve y = √x orthogonally is
The tangent and normal at P (t), for all real positive t, to the parabola y2 = 4ax meet the axis of the parabola in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle through the points P, T and G is
The two lines of regression are 2x - 7y + 6 = 0 and 7x – 2y +1 = 0. What is correlation coefficient between x and y ?
In a lottery 2000 tickets are sold and 50 equal prizes are rewarded. The probability of not getting a prize if you buy 1 ticket is:
AB, AC are tangents to a parabola y2 = 4ax. p1 p2 and p3 are the lengths of the perpendiculars from A, B and C respectively on any tangent to the curve, then p2, p1, p3 are in




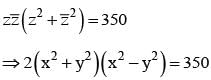
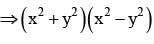
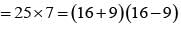
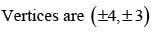
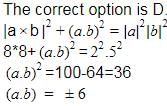
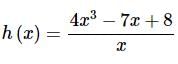
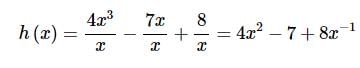
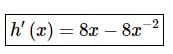
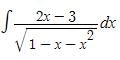
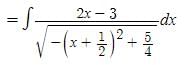
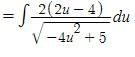
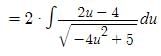
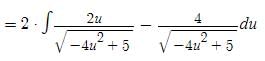
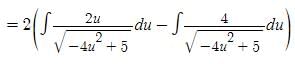
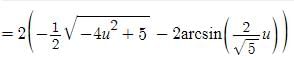
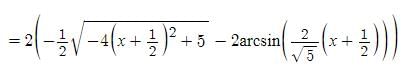
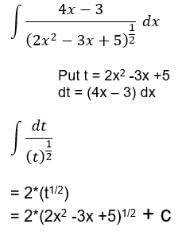
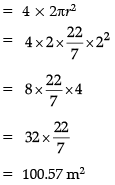
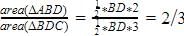
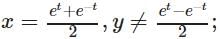 t ∈ R represents
t ∈ R represents